
8.若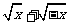 有意义,则
有意义,则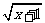 =
。
=
。
7.在数轴上表示 的点离原点的距离是
。
的点离原点的距离是
。
6. 的相反数是
;绝对值是
。
的相反数是
;绝对值是
。
5.在
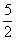 ,
,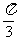 ,
,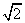 ,
, ,
,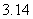 ,0,
,0, ,
,
 ,
,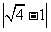 中,其中:
中,其中:
整数有 ;
无理数有 ;
有理数有 。
4.若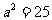 ,
,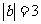 ,则
,则 ( )
( )
A. 8
B.±8
8
B.±8
C.±2 D.±8或±2
3.若 ,则
,则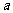 的值是( )
的值是( )
A. B.
B.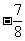
C.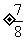 D.
D.
2. 的平方根是(
)
的平方根是(
)
A.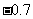 B.
B.
C.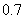 D.
D.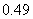
1. 有下列说法:
(1)无理数就是开方开不尽的数;
(2)无理数是无限不循环小数;
(3)无理数包括正无理数、零、负无理数;
(4)无理数都可以用数轴上的点来表示。
其中正确的说法的个数是( )
A.1 B.2 C.3 D.4
3.小结
(1)由现实情境出发,学习黄金分割、黄金比的概念;
(2)通过尝试、思考活动,认识黄金分割在几何中的一些应用.
2.探索活动
活动一 创设情境,引人黄金分割的概念.
关于黄金分割的概念,课本设计3幅图(芭蕾舞演员身体、东方明珠电视塔塔体、你最喜欢的矩形),让学生通过度量图中线段AB、BC(或AB、BC)的长度,计算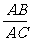 (或
(或 )的值的实践活动,引入黄金分割的概念.
)的值的实践活动,引入黄金分割的概念.
对于黄金分割的概念,课本把AB与AC的比值0.618称为黄金比.事实上,0.618只是黄金比的一个近似值,由于学生尚未学习一元二次方程,无法根据AB是BC、AC的比例中项的条件求出黄金比的准确值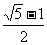 .教学时,不必补充相关知识,专门研究这一问题.
.教学时,不必补充相关知识,专门研究这一问题.
黄金分割既是比例线段的应用,又蕴含着丰富的文化价值.教学中,在向学生介绍它在生活中应用的同时,启发学生能根据已有的生活经验,列举一些黄金分割应用的实例.
活动二 通过尝试、思考活动,认识黄金分割在几何中的一些应用.
课本中“尝试”活动的目的在于:(1)向学生介绍一种作出黄金分割点的方法;(2)作为黄金分割在几何中的一个应用,介绍黄金三角形的概念,研究黄金三角形的性质,进一步巩固对黄金分割的认识.
课本中的“思考”活动,实际上是“尝试”活动的延伸.由于学生在“尝试”活动中已经研究了黄金三角形,知道顶角是36°的等腰三角形是黄金三角形,其底角的平分线与对边的交点是该边的黄金分割点,这样,要解决课本中提出的:图中点F、G、H、M、N分别是哪些线段的黄金分割点的问题,只要将问题转化为:(1)判断图中哪些三角形是黄金三角形?(2)点 F、G、H、M、N分别是哪些黄金三角形的底角的平分线与对边的交点?
由于学生还没有学习判定三角形相似的条件及其性质,对课本中“思考”活动的研究是通过黄金三角形的概念进行的,在学生系统地学习过判定三角形相似的条件及其性质之后,教师可引导他们利用黄金分割的概念和判定三角形相似的条件及其性质,判断图中的点F、G、H、M、N分别是哪些线段的黄金分割点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com