10.3 相似图形 同步练习

[目标与方法]

习题10.3　 1.(3) (4) 　2.

2、灵活选用代入消元法和加减消元法解二元一次方程组

1、掌握加减消元法解二元一次方程组

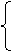解方程组：　 　

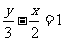
例1．解方程组　　 x+2y=1①

　　　　　　 　　　3x-2y=5②

解：①+②得，4x=6

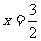
将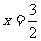代入①，得

解这个方程得：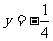　　

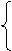所以原方程组的解是　

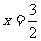
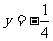
巩固练习(一)：练一练　 1.(1)

例2．解方程组　 5x-2y=4①

　　　　　　 　　　2x-3y=-5②

解：①×3，得

15x-6y=12③

②×3，得

4x-6y=-10 ④

③-④，得：

　　　　　 　　　　　　11x=22

　　　　 解这个方程得　　 x=2

将x=2代入①，得

5×2-2y=4

解这个方程得：　　　 y=3

所以原方程组的解是 　　x=2

y=3

巩固练习(二)：练一练　 1.(2)　 (3)　 (4) 　2.

3、这个方程组有何特点？

解法一：　 3x+2y=23①

　　　　　 5x+2y=33②

由①式得③

把③式代入②式

33

解这个方程得：　　　 y=4

把y=4代入③式

则　

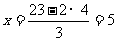
所以原方程组的解是　　 x=5

y=4

解法二：　 3x+2y=23①

　　　　　 5x+2y=33②

由①-②式：

3x+2y-(5x+2y)=23-33

3x-5x=-10

解这个方程得：　　　 x=5

把x=5代入①式，

3×5+2y=23

解这个方程得　　　　 y=4

　　　　　　 所以原方程组的解是　　 x=5

y=4

把方程组的两个方程(或先作适当变形)相加或相减，消去其中一个未知数，把解二元一次方程组转化为解一元一次方程，这种解方程组的方法叫做加减消元法(elimination by addition or subtraction) ，简称加减法.

活动一：1、上面“情境创设”中的方程，除了用代入消元法解以外，还有其他方法求解吗？

2、这些方法与代入消元法有何异同？

买3瓶苹果汁和2瓶橙汁共需要23元，买5瓶苹果汁和2瓶橙汁共需33元，每瓶苹果汁和每瓶橙汁售价各是多少？

设苹果汁、橙汁单价为x元，y元.

我们可以列出方程　　 3x+2y=23

　　　　　　　　　 　　　　5x+2y=33

问：如何解这个方程组？

P₁₁₂　 1、(1)(4)　 2、3、