2．能选择适当的方法判断三角形相似，灵活解决与三角形相似有关的问题．

[基础与巩固]

1．进一步通过实践与探索，得出两个三角形具备有两边对应成比例，并且夹角相等的条件，即可判断两个三角形相似的方法．

10.4探索三角形相似的条件(2) 同步练习

[目标与方法]

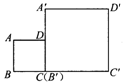
7．如图，已知正方形ABCD与正方形A′B′C′D′的边长比为1：2，请你利用这两个正方形，通过割补的方法，得到两个相似三角形，且相似比是1：3．

　　 要求：(1)借助原图拼图；

　　 (2)简要说明方法；

(3)指明相似的两个三角形．

[后花园]

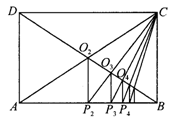
　　 智力操　 在美国的一堂数学课上，老师给同学们布置了一道“任意等分一条线段”的题．其中有一个学生用了一种与众不同的方法．他在纸上做出了如图所示的一个图形，他以老师给的已知线段AB为一条边作矩形ABCD，设AC、BD交于点O₂，作O₂P₂⊥AB，则垂足P₂就是AB的二等分点：连接CP₂交BD于点O₃，作O₃P₃⊥AB，则垂足P₃就是AB的三等分点；再依次做下去，就得到AB的四等分点，…n等分点．

　　 你能用所学过的知识解释其中的缘由吗？

6．(1)你能将一个直角三角形分割成两个三角形，并且使它们都与原三角形相似吗？试试看，在图①中画出你的设计方案；

(2)如果要将这个直角三角形分割成四个三角形，并且它们仍然都与原三角形相似，你还能做到吗？在图②中画画看!

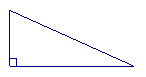
　　　　　　　　　 ①　　　　　　　　　　　　　　　　　 ②

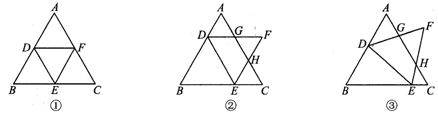
5．已知：如图，△ABC、△DEF均为等边三角形，点D、E分别在AB、BC上．

　　 (1)如图①，当D、E分别在AB、BC的中点时，图中有与△DBE相似的三角形吗？ 请你找出来，并选择一个说明理由；

　　 (2)如图②，当D、E分别从AB、BC的中点向点A、C以相同的速度运动时，图中有与△DBE相似的三角形吗？如果有，请你找出来，并选择一个说明理由；

(3)如图③，当D、E分别是AB、BC上的任意一点，(2)中的结果是否仍然成立？如果成立，请你找出来，并选择一个说明理由．

[拓展与延伸]

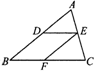
4．如图，在△ABC中，DE∥BC，EF∥AB，试说明△ADE∽△EFC．

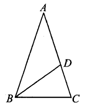
3．如图，在△ABC中，AB=AC，∠A=36°，BD是∠ABC的角平分线．△ABC与△BDC相似吗？请说明理由．

2．(1)具备下列各组条件的两个三角形中，不一定相似的是(　 )．

　　 (A)有一个角是40°的两个等腰三角形;　 (B)两个等腰直角三角形;

　　 (C)有一个角为100°的两个等腰三角形; (D)两个等边三角形

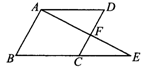
　(2)如图3，E是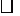ABCD的边BC的延长线上的一点，连接AE交CD于点F，图中的相似三角形有(　 )．

(A)1对　　 (B)2对　　 (C)3对　　 (D)4对

　　　　　　　　　 (3)　　　　　　　　　　　　　　 (4)

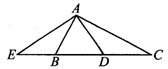
　 (3)如图4，在△ABC中，∠BAC=90°，D是BC的中点，AE⊥AD交CB的延长线于点E．下列结论正确的是(　 )．

　　 (A)△AED∽△ACB　　 (B)△AEB∽△ACD

　　 (C)△BAE∽△ACE　　 (D)△AEC∽△DAC

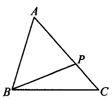
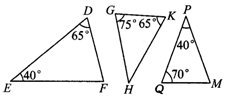
1．(1)已知：如图1，在△ABC中，∠A=40°，∠B=75°，图中各三角形中与△ABC相似的是________．

　　　　　　　　　　　 (1)　　　　　　　　　　　　　　　 (2)

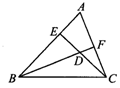
　　 (2)如图2，锐角△ABC的边AB、AC上的高CE和BF相交于点D，请写出图中的两对相似三角形：____________(用相似符号连接)．