2．能够选择适当的方法判定两个三角形相似，进一步解决与三角形相似有关的问题．

[基础与巩固]

1．通过对比和猜想，探索得出两个三角形有三边对应成比例，即可判断两个三角形相似的方法．

10.4 探索三角形相似的条件(3) 同步练习

[目标与方法]

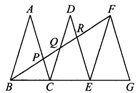
7．已知：如图，△ABC、△DCE、△FEG是3个全等的等腰三角形，边BC、CE、EG在一条直线上，且AB=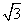，BC=1，连接BF，分别交AC、DC、DE于点P、Q、R．

　　 (1)△BFG与△FEG相似吗？请说明理由；

　　 (2)求BF的长；

(3)观察图形，请你提出一个与点P相关的问题，并进行解答．

[后花园]

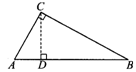
　　 妙趣角　 著名科学家爱因斯坦早在12岁时就利用相似三角形独立地证明了勾股定理．他认为：直角三角形的边的关系，必然是由其一锐角完全决定．

　　 爱因斯坦的方法是首先作出Rt△ABC(∠ACB=90°)的高CD．请你先找出图中的相似三角形，再利用它们来说明勾股定理：AC²+BC²=AB²．试试看!你也能行!

6．如图，AB⊥MN，CD⊥MN，垂足分别为B、D，AB=2，CD=4，BD=3．在直线MN上是否存在点P，能使△PAB∽△PCD？如果存在，满足上述条件的点P有几个？说明点P与点B、D的距离，并把图形画出来．

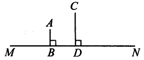
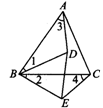
5．如图，D是△ABC内的一点，E是△ABC外的一点，且∠1=∠2，∠3=∠4，图中有与∠ACB相等的角吗？如果有，请找出来，并说明理由．

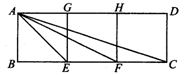
4．如图，四边形ABEG、GEFH、HFCD都是正方形，请你在图中找出一对相似比不等于1的相似三角形，并说明理由．

[拓展与延伸]

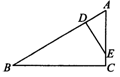
3．如图，在△ABC中，∠C=90°，点D、E分别在AB、AC上，且AD·AB=AF·AC．ED与AB垂直吗？请说明理由．

2．已知：在△ABC和△A′B′C′中，∠B=∠B′，AB=6，BC=8，B′C′=4，当A′B′=_______时，△ABC∽△A′B′C′．

1．如图，P是△ABC的边AC上的一点，连接BP．以下条件中，不能判定△ABP∽△ACB的是(　 )．

(A)

(C)∠ABP=∠C　　 (D)∠APB=∠ABC