2．在△ABC中，点D、E分别在AB、AC上，AD=4，DB=2，AC=8．当AE=______时，△ADE∽△ABC；当AE=_______时，△ADE∽△ACB．

1．根据下列条件，试判别△A′B′C′与△ABC是否相似，并说明理由：

　 (1)∠A=70°，∠C=65°，∠A′=70°，∠B′=35°；

　 (2)∠B=55°，AB=6cm，BC=7cm，∠B′=55°，A′B′=18cm，B′C′=21cm；

　 (3)AB=10cm，BC=8cm，AC=16cm，A′B′=16cm，B′C′=12.8cm，A′C′=25.6cm．

2．通过对具体问题的分析和思考，提高分析问题和解决问题的能力．

[基础与巩固]

1．灵活运用三角形相似的不同条件解决问题，进一步体会判断三角形相似的各种方法的特征．

10.4 探索三角形相似的条件(4)同步练习

[目标与方法]

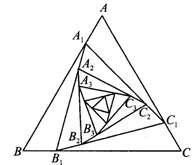
5．如图，小辉在图纸上画了一个等边三角形ABC，接着在AB、BC、CA上分别取点A₁、B₁、C₁，且AA₁=BB₁=CC₁，得到△A₁B₁C₁；再在A₁B₁、B₁C₁、C₁A₁上分别取点A₂、B₂、C₂，且A₁A₂=B₁B₂=C₁C₂，得到△A₂B₂C₂…按此方法，小辉画出了一个非常漂亮的几何图案，小辉发现图案中的△ABC、△A₁B₁C₁、△A₂B₂C₂…都是相似三角形，请你以△ABC和△A₁B₁C₁为例说明其中的原因．

4．强强为了装饰自己的房间，想要制作两个三角形的框架，其中一个三角形框架的三边长分别为4、5、6，另一个三角形框架的一边长为2．你认为他可以如何选料使这两个三角形相似？

[拓展与延伸]

3．已知：在△ABC中，AB=4，BC=5，CA=6．

　　 (1)如果DE=10，那么当EF=_______，FD=______时，△DEF∽△ABC；

　　 (2)如果DE=10，那么当EF=_______，FD=______时，△FDE∽△ABC．

2．(1)在△ABC中，AB：BC：CA=2：3：4，在△A′B′C′中，A′B′=1，C′A′=2，当B′C′=_____时，△ABC∽△A′B′C′．

　 (2)在△ABC中，AB=6，AC=8，在△A′B′C′中，A′B′=4，A′C′=3，若BC：B′C′=________，则△ABC∽△_______．

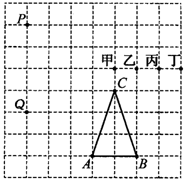
1．(1)如图，若A、B、C、P、Q、甲、乙、丙、丁都是方格纸的格点，为使△ABC∽△PQR，则点R应是甲、乙、丙、丁4点中的(　 )．

(A)甲　　 (B)乙　　　 (C)丙　　　 (D)丁

　(2)下面给出4个结论：①所有的等腰三角形都相似；②所有的直角三角形都相似；③所有的等边三角形都相似；④所有的矩形都相似．

　　 其中，正确的有(　 )．

　　 (A)1个　　 (B)2个　　　 (C)3个　　　 (D)4个