3．例题教学

　　 例1是复习巩固判定三角形相似的条件．其中，求上C的度数的根据是：三角形3个内角的和等于 180°；判定△ABC∽△A’B’C’的根据是：两个角对应相等的两个三角形相似．

　　 例2的解答过程实际上仅说明当平行于三角形一边的直线与其他两边相交时，所构成的三角形与原三角形相似．当平行于三角形一边的直线与其他两边的延长线相交、与其他两边的反向延长线相交的情况，由学生思考、解答．

　　 课本通过例题、思考等数学活动，归纳出判定三角形相似的条件：平行于三角形一边的直线与其他两边相交，所构成的三角形与原三角形相似．由于这一判定三角形相似的条件在实际应用中用途较广，教学时应结合实例向学生说明，在三角形中“见平行，想相似”，也是解题的一般思路．

2．探索活动

　　 探索活动分为5个层次．

　　 第一层次：与判定两个三角形全等的条件类比，使学生感悟到，判定两个三角形相似也可以适当减少条件，提高学生探索两个三角形相似的条件的主动性．

　　 第二层次：组织操作活动，画出图中的3个三角形．

　　 第三层次：组织思考活动．学生通过实际度量图10-10(1)与图10-10(3)中三角形的边长与角的度数，发现这两个三角形的对应角相等、对应边成比例，它们是相似的．而此时图中给出的条件仅为：

　　 ∠A”＝∠A，∠B”＝∠B，A”B”＝2AB．

　　 第四层次：改变兑值的大小(∠A”＝∠A，∠B”＝∠B的条件不变)，度量画出的两个三角形的边和角，发现仍然满足相似的条件，这样使学生感悟到：只要满足∠A”＝∠A，∠B”＝∠B的条件，图10-10(1)与图10-10(3)的三角形相似．

　　 第五层次：通过探索活动，归纳判定三角形相似的条件(1)．

1．情境创设

　　 前面我们学习了相似三角形的概念，即三个角对应相等、三条边对应成比例的两个三角形是相似三角形，同时这也是判定两个三角形相似的一种方法．除此之外，还有没有其他的判定方法呢?

2．经历“操作一观察一探索一说理”的数学活动过程，发展合情推理和有条理的表达能力．

[教学过程(第一课时)]

1．探索三角形相似的条件，会运用三角形相似的条件解决有关问题．

10．4　探索三角形相似的条件

第一课时

[教学目标]

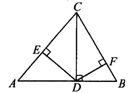
6．如图，在△ABC中，CD⊥AB，DE⊥AC，DF⊥BC，垂足分别为D、E、F．

　　 (1)CA·CE与CB·CF相等吗？为什么？

(2)连接EF交CD于点O，线段OC、OD、OE、OF成比例吗？

[后花园]

　　 智力操 　在△ABC中，点P是BA延长线上的一点．

　　 请你设计合理的方案来确定点P的位置：(1)使BC是AB与BP的比例中项；(2)使AC是AB与AP的比例中项．

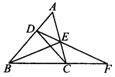
5．如图，在△ABC中，点D、E分别在边AB、AC上，连接并延长DE交BC的延长线于点F，连接DC、BE．若∠BDE+∠BCE=180°．

　 (1)写出图中3对相似三角形(注意：不得添加字母和线)；

(2)请在你所找出的相似三角形中选取1对，说明它们相似的理由．

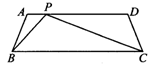
4．如图，在梯形ABCD中，AD∥BC，AD<BC，AD=5，AB=DC=2，P为AD上的一点，∠BPC=∠A．△ABP与△DPC相似吗？为什么？

[拓展与延伸]

3．(1)P是Rt△ABC的斜边BC上异于点B、C的一点，过点P作直线截△ABC，使截得的三角形与△ABC相似，满足这样条件的直线共有(　 )．

　　 (A)1条　　 (B)2条　　 (C)3条　　 (D)4条

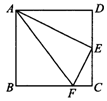
　(2)如图，在正方形ABCD中，E是CD的中点，FC=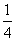BC．图中与△ADE相似的三角形有( )．

(A)0个　　 (B)1个　　 (C)2个　　 (D)3个