2.有两个矩形,第一个矩形的长、宽比第二个矩形的长、宽都长1,第一个矩形的长比宽与第二个矩形的长比宽都长1,第一个矩形的周长比第二个矩形的周长大4,求这两个矩形的面积.
①学生自探
②再组织学生议一议,在四人小组中发表自己的意见。
由学生填
能
学生板演
学生观察
回答
充分发挥学生的作用
P117 1 ,2
|
作业
|
P120 2 ,4
|
板 书
设 计
|
问题3
问题4
分析:
分析:
解题过程
解题过程
|
教 学
后 记
|
|
课
题
|
第十章二元一次方程组
|
课时分配
|
本课(章节)需 3 课时
本 节 课 为 第 1 课时
为 本 学期总第 课时
|
10.4用方程组解决问题
|
教学目标
|
1.使学生读完题后会说题。找出等量关系。
2.鼓励学生主动探索。有了答案后,引导学生合作交流,择优。
|
重
点
|
理解题意,找出数量关系
|
难
点
|
找出等量关系。
|
教学方法
|
讲练结合、探索交流
|
课型
|
新授课
|
教具
|
投影仪
|
教
师 活 动
|
学 生 活 动
|
情景设置:
操作多媒体出示图像,提出问题。
国庆长假期间,某旅行社接待一日游和三日游的游客共2200人,收旅行费200万元,其中一日游每人收费200元,三日游每人收费1500元。该旅行社接待的一日游和三日游旅客个多少人?
提出问题
(1)有几个未知数?几个已知量?
(2)已知量和未知量之间的数量关系你能找到吗?
(3)相等的关系是否明显?你找找。
新课讲解:
探索解决问题的方法
你能告诉我等量关系或方程吗?
① 人数等量关系
② 钱数相等关系
板书:
解:设接待一日游旅客x人,三日游旅客y人
那么一日游共收费200x元,三日游共收费1500y元。
由题意得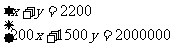
解这个方程组得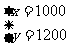
答:该旅行社接待一日游旅客1000人,三日游旅客1200人。
想一想:还有其他的方法吗?
应用举例
为了保护环境,某学校环保小组成员收集废旧电池,第一天收集5节1号电池,6节5号电池,总质量为500g;第二天收集3节一号电池,4节5号电池,总质量为310g。一节一号电池和一节五号电池的质量分别是多少?
解:设一节一号电池的质量为xg,一节五号电池的质量是yg。
由题意得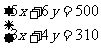
解这个方程得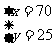
答:一节一号电池的质量为70g,一节五号电池的质量是25g。
废旧电池的危害请同学们“读一读”P114.
练一练:
小结:
题目中的数量关系有的明显,有的不明显,一定要加以分析。文字语言,符号语言相互转换是数学建模的过程,培养学生的能力。
教学素材:
A组题:
1.七年一班共44人,现分成甲、乙两组参加学校活动。由于需要,现从乙组调了6人到甲组后,甲乙两组人数相等。问原来甲乙各多少人?
2.小亮买了5本练习本和2支圆珠笔共花了5.5元。已知圆珠笔比练习本贵1元,问练习本和圆珠笔各多少元?
3.现有邮票一打,已知面值为一元和两元的,总面值为50元,2元的邮票比1元的邮票多10张,问面值为一元和两元的邮票各多少张?
4.一长方形周长为24,现把长增加3,宽不变,周长变为30。问原来的长、宽为多少?
5.若甲数比乙数的2倍小3,且甲、乙两数的和是9,求甲、乙两数。
B组题:
1.一长方形周长为24,现把长、宽都增加3,周长变为36。求原来长方形的面积。
2.一个两位数,其个位与十位的数字之和为6。现把十位数字与个位数字对调,产生的新的两位数比原来的两位数大18。求原来的两位数。
|
观察图形
回答问题
①学生自探
②再组织学生讨论,鼓励学生自述
学生板演
鼓励学生用一元一次方程解出
鼓励学生读题,只探,交流,找出等量关系
P115 1.2
|
作业
|
P120 1,6
|
板 书
设 计
|
问题一
问题二
解题过程:
解题过程:
练习
|
教 学
后 记
|
|
课
题
|
第十章二元一次方程组
|
课时分配
|
本课(章节)需 2 课时
本 节 课 为 第 2 课时
为 本 学期总第 课时
|
10.3解二元一次方程组(加减消元法)
|
教学目标
|
1.使学生会用加减法解二元一次方程组。
2.学生通过解决问题,了解代入法与加减法的共性及个性。
|
重
点
|
探寻用加减法解二元一次的方程组的进程。
|
难
点
|
消元转化的过程
|
教学方法
|
讲练结合、探索交流
|
课型
|
新授课
|
教具
|
投影仪
|
教
师 活 动
|
学 生 活 动
|
情景设置:
小明买了两份水果,一份是3kg苹果、2kg香蕉,共用去13.2元;另一份是2kg苹果、5kg香蕉,共用去19.8元。设苹果x元/kg,香蕉y元/kg.列出方程。
新课讲解:
列出方程组
1.解方程组
分析:关键的出方程〈1〉中的2y与方程〈2〉中的-2y互为相反数。想象出如果相加两个方程,会是什么结果?
板演:
解:〈1〉+〈2〉得:
4x=6
x=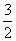
把x=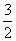 代入〈1〉得 代入〈1〉得
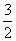 +2y=1 +2y=1
解出这个方程,得
y=
所以原方程组的解是
2.解方程组
通过议一议,让学生都有感觉消去含x或y的项都可以,但哪个更简便?
解:〈1〉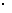 3,得 3,得
15x-6y=12 〈3〉
〈2〉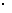 2,得 2,得
4x-6y=-10 〈4〉
〈3〉-〈4〉,得
11x=22
x=2
将x=2代入〈1〉,得
5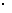 2-2y=4 2-2y=4
y=3
所以原方程组的解是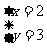
加减消元法:把方程组的两个防城(或先作适当变形)相加或相减,消去其中一个未知数,把解二元一次方程组转化为解一元一次方程。
练一练:
解方程组
小结:
加减消元法关键是如何消元,化二元为一元。
先观察后确定消元。
教学素材:
A组题:解下列方程组:
(1)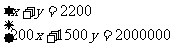
(2)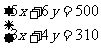
(3)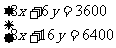
(4)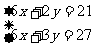
(5)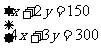
B组题:运用“转化”的思想方法,你能解下面的三元一次方程组吗?
(1)
(2)
|
学生读题,议一议
学生想一想,如感到困难则看道简单题。
由学生观察,如何求出x,y的值,学生再讨论。
试一试。学生口述。
老师板演
得到一元一次方程
学生再观察,议一议
①消去哪个未知数
②怎样消去?
P112 1(1)(2)(3)(4)
|
作业
|
习题11.3 P112 1(3)(4) 3 , 4
|
板 书
设 计
|
方程组 解方程组 解方程组
(1)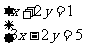
(2)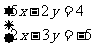
(3) 
|
教 学
后 记
|
|
课
题
|
第十章二元一次方程组
|
课时分配
|
本课(章节)需 2 课时
本 节 课 为 第 2 课时
为 本 学期总第 课时
|
10.3解二元一次方程组(加减消元法)
|
教学目标
|
1.使学生会用加减法解二元一次方程组。
2.学生通过解决问题,了解代入法与加减法的共性及个性。
|
重
点
|
探寻用加减法解二元一次的方程组的进程。
|
难
点
|
消元转化的过程
|
教学方法
|
讲练结合、探索交流
|
课型
|
新授课
|
教具
|
投影仪
|
教
师 活 动
|
学 生 活 动
|
情景设置:
小明买了两份水果,一份是3kg苹果、2kg香蕉,共用去13.2元;另一份是2kg苹果、5kg香蕉,共用去19.8元。设苹果x元/kg,香蕉y元/kg.列出方程。
新课讲解:
列出方程组
1.解方程组
分析:关键的出方程〈1〉中的2y与方程〈2〉中的-2y互为相反数。想象出如果相加两个方程,会是什么结果?
板演:
解:〈1〉+〈2〉得:
4x=6
x=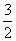
把x=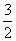 代入〈1〉得 代入〈1〉得
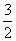 +2y=1 +2y=1
解出这个方程,得
y=
所以原方程组的解是
2.解方程组
通过议一议,让学生都有感觉消去含x或y的项都可以,但哪个更简便?
解:〈1〉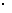 3,得 3,得
15x-6y=12 〈3〉
〈2〉 2,得 2,得
4x-6y=-10 〈4〉
〈3〉-〈4〉,得
11x=22
x=2
将x=2代入〈1〉,得
5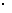 2-2y=4 2-2y=4
y=3
所以原方程组的解是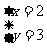
加减消元法:把方程组的两个防城(或先作适当变形)相加或相减,消去其中一个未知数,把解二元一次方程组转化为解一元一次方程。
练一练:
解方程组
小结:
加减消元法关键是如何消元,化二元为一元。
先观察后确定消元。
教学素材:
A组题:解下列方程组:
(1)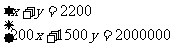
(2)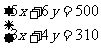
(3)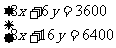
(4)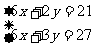
(5)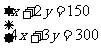
B组题:运用“转化”的思想方法,你能解下面的三元一次方程组吗?
(1)
(2)
|
学生读题,议一议
学生想一想,如感到困难则看道简单题。
由学生观察,如何求出x,y的值,学生再讨论。
试一试。学生口述。
老师板演
得到一元一次方程
学生再观察,议一议
①消去哪个未知数
②怎样消去?
P112 1(1)(2)(3)(4)
|
作业
|
习题11.3 P112 1(3)(4) 3 , 4
|
板 书
设 计
|
方程组 解方程组
解方程组
(1)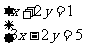
(2)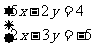
(3) 
|
教 学
后 记
|
|
课
题
|
第十章二元一次方程组
|
课时分配
|
本课(章节)需 2 课时
本 节 课 为 第 2 课时
为 本 学期总第 课时
|
10.3解二元一次方程组(加减消元法)
|
教学目标
|
1.使学生会用加减法解二元一次方程组。
2.学生通过解决问题,了解代入法与加减法的共性及个性。
|
重
点
|
探寻用加减法解二元一次的方程组的进程。
|
难
点
|
消元转化的过程
|
教学方法
|
讲练结合、探索交流
|
课型
|
新授课
|
教具
|
投影仪
|
教
师 活 动
|
学 生 活 动
|
情景设置:
小明买了两份水果,一份是3kg苹果、2kg香蕉,共用去13.2元;另一份是2kg苹果、5kg香蕉,共用去19.8元。设苹果x元/kg,香蕉y元/kg.列出方程。
新课讲解:
列出方程组
1.解方程组
分析:关键的出方程〈1〉中的2y与方程〈2〉中的-2y互为相反数。想象出如果相加两个方程,会是什么结果?
板演:
解:〈1〉+〈2〉得:
4x=6
x=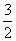
把x=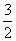 代入〈1〉得 代入〈1〉得
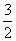 +2y=1 +2y=1
解出这个方程,得
y=
所以原方程组的解是
2.解方程组
通过议一议,让学生都有感觉消去含x或y的项都可以,但哪个更简便?
解:〈1〉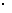 3,得 3,得
15x-6y=12 〈3〉
〈2〉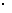 2,得 2,得
4x-6y=-10 〈4〉
〈3〉-〈4〉,得
11x=22
x=2
将x=2代入〈1〉,得
5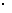 2-2y=4 2-2y=4
y=3
所以原方程组的解是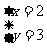
加减消元法:把方程组的两个防城(或先作适当变形)相加或相减,消去其中一个未知数,把解二元一次方程组转化为解一元一次方程。
练一练:
解方程组
小结:
加减消元法关键是如何消元,化二元为一元。
先观察后确定消元。
教学素材:
A组题:解下列方程组:
(1)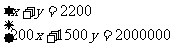
(2)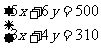
(3)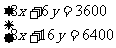
(4)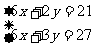
(5)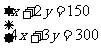
B组题:运用“转化”的思想方法,你能解下面的三元一次方程组吗?
(1)
(2)
|
学生读题,议一议
学生想一想,如感到困难则看道简单题。
由学生观察,如何求出x,y的值,学生再讨论。
试一试。学生口述。
老师板演
得到一元一次方程
学生再观察,议一议
①消去哪个未知数
②怎样消去?
P112 1(1)(2)(3)(4)
|
作业
|
习题11.3 P112 1(3)(4) 3 , 4
|
板 书
设 计
|
方程组 解方程组
解方程组
(1)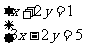
(2)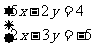
(3) 
|
教 学
后 记
|
|
课
题
|
第十章二元一次方程组
|
课时分配
|
本课(章节)需 2 课时
本 节 课 为 第 1 课时
为 本 学期总第 课时
|
10.3解二元一次方程组(代入消元法)
|
教学目标
|
1.学生会用代入法解二元一次方程组。
2.学生通过解决问题,了解解二元一次方程组的必要性。
|
重
点
|
探寻用代入法解二元一次的方程组的进程。
|
难
点
|
消元转化的过程
|
教学方法
|
讲练结合、探索交流
|
课型
|
新授课
|
教具
|
投影仪
|
教
师 活 动
|
学 生 活 动
|
情景设置:
从学生熟悉的情景引入课题。
(1)
根据篮球比赛规则:赢一场得2分,输一场得1分,在一次中学生篮球联赛中,某球队赛了12场。设赢了x场,输了y场,积20分,列出方程。
(2)
小亮在“智力快车”竞赛中回答10个问题,答对一题得4分,答错一题扣1分,他共得25分,设小亮答对x题、答错y题,列出二元一次方程。
新课讲解:
(1)解方程组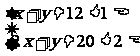
分析:如何解出x,y?设想能把二元化为一元,由学生自己讨论。
解:由〈1〉得:y=12-x 〈3〉
把〈3〉代入〈2〉,得
2x+12-x=20
解这个一元一次方程得
x=8
把x=8代入〈3〉,得
y=4
所以原方程的解是
(2)解方程: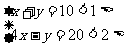
老师板演:
解:由〈1〉得x=10-y 〈3〉
把〈3〉代入〈2〉,得
4(10-y)-y=20
解这个一元一次方程,得
y=4
把y=4代入〈3〉,得
x=6
所以原方程组的解是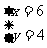
练一练:
小结:
代入消元法的方法。
通过“议一议”、“说一说”让学生切实体会到代入消元法的思想“二元转化为一元”。
教学素材:
A组题:
代入法解下列方程组:
(1)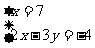
(2)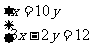
(3)
(4)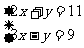
(5)
B组题
1.已知: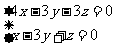 ,并且 ,并且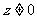
求:x:y与y:z.
2.编写一道以(-3,1)为解的二元一次方程组。
|
学生列方程
语言表达
为何不代入〈2〉
学生议一议。
为何代入〈3〉?
学生议一议。
学生讨论
学生口述
P110 试一试
P110“练一练”1
|
作业
|
P112练一练1(1)
习题11.3 1(1)(2)(4).2
|
板 书
设 计
|
多媒体演示
(1)解方程组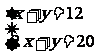 解题步骤
解题步骤
(1)
(2)解方程组
(2)
|
教 学
后 记
|
|
|
|
|
|
|
|
|
|
|

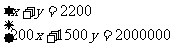
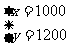
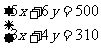


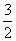
 代入〈1〉得
代入〈1〉得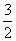 +2y=1
+2y=1


 3,得
3,得 2,得
2,得 2-2y=4
2-2y=4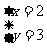

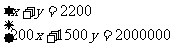
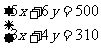
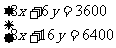
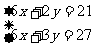
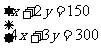


 解方程组
解方程组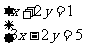
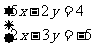



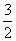
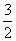 代入〈1〉得
代入〈1〉得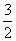 +2y=1
+2y=1


 3,得
3,得 2,得
2,得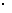 2-2y=4
2-2y=4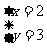

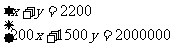
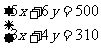
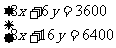
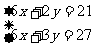
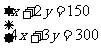


 解方程组
解方程组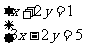
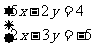



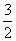
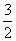 代入〈1〉得
代入〈1〉得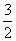 +2y=1
+2y=1


 3,得
3,得 2,得
2,得 2-2y=4
2-2y=4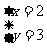

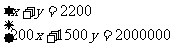
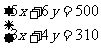
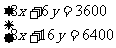
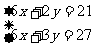
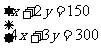


 解方程组
解方程组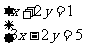
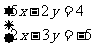

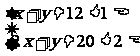

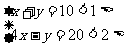
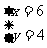
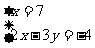
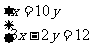

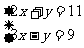

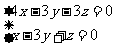 ,并且
,并且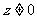
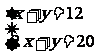 解题步骤
解题步骤
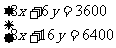
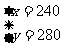
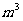 时,按基本价格收费,该市某户居民今年4、5月份的用水量和水费如下表所示,试求用水收费的两种价格。
时,按基本价格收费,该市某户居民今年4、5月份的用水量和水费如下表所示,试求用水收费的两种价格。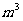
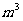 ,所以水费有两部分组成21元。
,所以水费有两部分组成21元。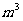 ,所以水费有两部分组成27元。
,所以水费有两部分组成27元。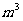 ;超过6
;超过6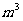 部分的按y元/
部分的按y元/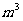 .
.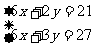

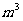 ;超过6
;超过6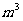 部分的按6元/
部分的按6元/