1、通过实践与探索，得出相似三角形的周长及面积与相似比的关系.

对相似形性质的探究,往往是不容易引起学生的兴趣,为此,本节课通过求“地块的实际周长与面积”这一情境,利用问题的设计,激发学生探究这一空白知识的欲望.再让学生通过“操作--观察--探究--说理”这一过程,发现相似多边形的周长与相似比的关系,进而通过合情推理,利用设参数的思想,探索得出相似三角形的周长与相似比的关系；再运用类比的思想,进一步的探究相似三角形、相似多边形的面积比与相似比的关系.在教学中，一定要给学生充分的探索、思考时间，尤其是知识的形成，切不可强行灌输，草草了事，只有让学生明白其根源，才能得以自如的运用，进而更有效地培养学生合情推理和有条理的表达能力.

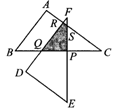
6．如图，在Rt△ABC中，∠A=90°，AB=3cm，AC=4cm，以斜边BC上距点B3cm的点P为中心，把这个三角形按逆时针方向旋转90°成图中的△DEF位置，求旋转前后两个直角三角形重叠部分的面积是多少？

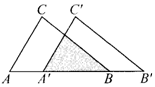
5．如图，把△ABC沿边AB平移到△A′B′C′的位置，它们重叠部分(即图中的阴影部分)的面积是△ABC的面积的一半，若AB=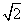，求此三角形移动的距离AA′的长．

4．已知△ABC的三边长分别为3，4，5，与它相似的△A′B′C′的最大边长为15，求△A′B′C′的面积．

[拓展与延伸]

3．在一张比例尺为1：5 000的地图上，一块多边形区域的周长是72cm，面积是320cm²，求这个区域的实际周长和面积．

2．(1)等腰三角形ABC的腰的长为12，底的长为10，等腰三角形A′B′C′的两边长分别为5和6，且△ABC∽△A′B′C′，则△A′B′C′的周长为(　 )．

　　 (A)17　　　 (B)16　　　 (C)17或16　　 (D)34

　 (2)两个相似多边形的一组对应边分别为3cm和4.5cm，如果它们的面积和为78cm²，那么较大的多边形面积为(　 )．

　　 (A)46.8cm²　　 (B)42cm²　　 (C)52cm²　　 (D)54cm²

1．(1)已知△ABC∽△A′B′C′，且AB=2A′B′，如果△ABC的周长是26cm，那么△A′B′C′的周长是______cm；

　 (2)把一个四边形放大成与其相似的四边形，如果边长扩大为原来的10倍，那么面积扩大为原来的________倍，如果面积扩大为原来的25倍，那么边长扩大为原来的_________倍；

　 (3)要把一根1m长的铜丝截成两段，用它们围成两个相似三角形，且相似比为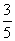，那么截成的两段铜丝长度的差应是______m．

2．运用类比的方法，得出相似多边形的周长比及面积比与相似比的关系．

[基础与巩固]

1．通过实践与探索，得到相似三角形的周长比及面积比与相似比的关系．