
对相似三角形对应线段(高、中线、角平分线)的比等于相似比这一性质的研究,首先通过创设“在三角形中如何截得规定的正方形”这一问题情境,让学生感受到解决该实际问题的困难,从而激发学生探究新知识的兴趣和热情,再让学生在相似三角形的概念及判定三角形相似的条件的基础上,进一步运用类比的思想探索研究相似三角形的性质:相似三角形的对应线段(高、中线、角平分线)的比等于相似比,学生由全等三角形的对应线段都相等,通过类比不难猜想得出相似三角形的这一性质,进而通过“操作--观察--探究--说理”的教学活动过程进行验证.在教学中,一定要让学生充分经历探究相似三角形这一性质的数学活动过程,以发展学生的合情推理和有条理的表达能力,最后,通过应用提高学生的知识运用能力,并感受到学习本节知识的应用价值.
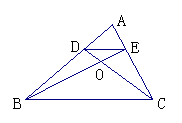
2、如图,在△ABC中,DE//BC,若AE/EC=1/2,试求△DOE与△BOC的周长比与面积比.
1、P131 练习1、2、3
例1. 在比例尺为1:500的地图上,测得一个三角形地块ABC的周长为12cm,面积为6cm2,求这个地块的实际周长为面积.
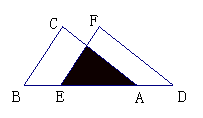
 例2. 如图,把△ABC沿AB边平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC的面积的一半,若AB=2,求此三角形移动的距离AD的长.
例2. 如图,把△ABC沿AB边平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC的面积的一半,若AB=2,求此三角形移动的距离AD的长.
(例2) (拓展练习2)
说明:“相似三角形的面积比等于相似比的平方”是一个难点,学生不易把握,通过这个例题,进一步巩固这个难点,让学生切实理解相似三角形的面积比与相似比(即对应边的比)的关系.
情境1:在比例尺为1:500的地图上,测得一个三角形地块ABC的周长为12cm,面积为6cm2,求这个地块的实际周长及面积.
问题1. 在这个情境中,地图上的三角形地块与实际地块是什么关系? 1:500表示什么含义?
问题2. 要解决这个问题,需要什么知识?
问题3. 在没有了解这些知识前,你能对这个地块的实际周长与面积作出估计吗?
问题4. 如何说明你的猜想是否正确呢?
情境2:(课本P101)章头图图(3)和图(4)中的相似多边形.
问题1. 你能通过操作、观察、归纳、思考发现这两个相似多边形的周长比与它们的相似比的关系吗?
问题2. 方格纸中的相似多边形的周长比与相似比是相等的,那么其它的相似形呢?比如相似三角形呢?
情境3:若△ABC∽△A′B′′C,那么△ABC与△A′B′C′的周长比等于相似比吗?
问题1. 为了解决这个问题,不妨设这个相似比为k,只要考虑什么就可以了?
问题2. 相似比为k,那么哪些线段的比也等于k?
问题3. 这两个三角形的周长又分别与哪些线段有关?
问题4. 如何得出这两个三角形的周长比与相似比k的关系?
得出:相似三角形的周长比等于相似比
问题5. 你能运用类似的方法说明“相似多边形的周长等于相似比吗?”
得出:相似多边形的周长等于相似比
情境4:若△ABC∽△A′B′C′,那么△ABC与△A′B′C′的面积比与相似比又有什么关系呢?
问题1. 有了前面探究的经验,你能想到一个合理的方法来研究这个问题吗?
问题2. 若AD与A′D′是这两个三角形的高,你知道AD与A′D′的比与相似比k的关系吗?能说明理由吗?
问题3. 你能说明这两个三角形面积比与相似比的关系吗?
得出:相似三角形的面积比等于相似比的平方
问题4:你能类似地得出相似多边形的面积比与相似比的关系吗?得出:相似多边形的面积比等于相似比的平方.
1.两个相似五边形的面积比为16:25,其中较大的五边形的周长为30cm,则较小 的五边形的周长为______ cm.
 2.如图,在△ABC中,DE//BC,若AE/EC=1/2,试求△DOE与△BOC的周长比与面积比. 2.如图,在△ABC中,DE//BC,若AE/EC=1/2,试求△DOE与△BOC的周长比与面积比.
第2题图 第3题图 3.四边形 ABCD是平行四边形,点E是BC的延长线上的一点,而且CE:BC=1:3,若△DGF的面积为9,试求:(1)△ABG的面积.(2)△ADG与△BGE的周长比和面积比. 说明:此练习仅仅作为课本P131练习的补充,教者可在用完书上练习后选择使用. |
|
|
例1. 在比例尺为1:500的地图上,测得一个三角形地块ABC的周长为12cm,面积为6cm2,求这个地块的实际周长为面积. 说明:这实际上就是情境1的问题,目的是让学生能运用所探索的新知识,来解决这个问题,教学中应鼓励独立思考,自主完成,教师作规范书写的指导. 例2.在△ABC中,D、E、F是AB、AC、BC的中点,求△DEF与△ABC的周长比和面积比. 例3. 如图,把△ABC沿AB边平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC的面积的一半,若AB=2,求此三角形移动的距离AD的长.  说明:“相似三角形的面积比等于相似比的平方”是一个难点,学生不易把握,通过这个例题,进一步巩固这个难点,让学生切实理解相似三角形的面积比与相似比(即对应边的比)的关系. |
|
|
活 动 内 容 |
师生互动思考与安排 |
|
情境1:在比例尺为1:500的地图上,测得一个三角形地块ABC的周长为12cm,面积为6cm2,求这个地块的实际周长及面积. 问题1. 在这个情境中,地图上的三角形地块与实际地块是什么关系? 1:500表示什么含义? 问题2. 要解决这个问题,需要什么知识? 问题3. 在没有了解这些知识前,你能对这个地块的实际周长与面积作出估计吗? 问题4. 如何说明你的猜想是否正确呢? 说明:通过这个情境,目的是为了让学生了解学习相似三角形的性质是生活的需要.问题1要求学生知道这两个地块是相似的,比例尺1:500就是它们的相似比;问题2要求学生对所需知识作出一个估计;问题3是让学生在缺少这些知识的情况下作出一个猜想,让学生能感知要求这地块的实际周长及面积与相似比1:500有关;问题4是激发学生探索新知,验证自己猜想的欲望,同时揭开本节课所要学习内容的实质. 情境2:(课本P101)章头图图(3)和图(4)中的相似多边形. 问题1. 你能通过操作、观察、归纳、思考发现这两个相似多边形的周长比与它们的相似比的关系吗? 说明:通过这个情境,目的是让学生能利用合情推理,得出相似多边形的周长比等于相似比,必要时,可让学生合作交流共同探索. 活 动 内 容 |
师生互动思考与安排 |
|
问题2. 方格纸中的相似多边形的周长比与相似比是相等的,那么其它的相似形呢?比如相似三角形呢? 说明:通过问题2,让学生经历从特殊到一般的思维过程. 情境3:若△ABC∽△A’B’C’,那么△ABC与△A’B’C’的周长比等于相似比吗? 问题1. 为了解决这个问题,不妨设这个相似比为k,只要考虑什么就可以了? 问题2. 相似比为k,那么哪些线段的比也等于k? 问题3. 这两个三角形的周长又分别与哪些线段有关? 问题4. 如何得出这两个三角形的周长比与相似比k的关系? 说明:通过这几个问题,目的是引导学生运用设参数的思想,通过合情推理,探索出“相似三角形的周长比等于相似比”这一结论. 问题5. 你能运用类似的方法说明“相似多边形的周长等于相似比吗?” 说明:引导学生运用类比的思想探索出“相似多边形的周长等于相似比”的合理性. 情境4:若△ABC∽△A’B’C’,那么△ABC与△A’B’C’的面积比与相似比又有什么关系呢? 问题1. 有了前面探究的经验,你能想到一个合理的方法来研究这个问题吗? 说明:通过这个问题,让学生能够主动设计探究的方法,引导学生设出参数,并考虑要得出这两个比的关系,必须与三角形的高产生联系. 问题2. 若AD与A’D’是这两个三角形的高,你知道AD与A’D’的比与相似比k的关系吗?能说明理由吗? 问题3. 你能说明这两个三角形面积比与相似比的关系吗? 说明:通过这两个问题,引导学生通过合情推理,得出AD与A’D’的比与相似比k相等的关系.学生可以通过合作交流,找出解决问题的方法,说理过程应分3步: 第一, 根据题设条件说明这两个直角三角形相似; 第二, 由两个直角三角形相似得对应线段成比例; 第三,利用三角形面积公式,得出相应结论. 问题4:你能类似地得出相似多边形的面积比与相似比的关系吗?通过章头图,大家可以验证一下. 说明:再一次运用类比的思想,自我探索相似多边形的面积比. |
|
3、经历“操作--观察--探索--说理”的数学活动过程,发展合理推理和有条理的表达能力.
2、运用类比的思想方法,得出相似多边形的周长及面积与相似比的关系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com