练习册

  • 练习册
  • 试题
     0  202398  202406  202412  202416  202422  202424  202428  202434  202436  202442  202448  202452  202454  202458  202464  202466  202472  202476  202478  202482  202484  202488  202490  202492  202493  202494  202496  202497  202498  202500  202502  202506  202508  202512  202514  202518  202524  202526  202532  202536  202538  202542  202548  202554  202556  202562  202566  202568  202574  202578  202584  202592  447090 

    1.课本P132页第1题和P133页第2题.

    试题详情

    例1. 课本P132例2

    例2. (情境一中的问题)

    变式训练：课本P134页第6题.

    试题详情

    问题1. 全等三角形的对应线段(如高、中线、角平分线)有怎样的关系？怎样说理，选举其中一例加以说明.

    问题2. 相似三角形的对应边成比例，对应线段有怎样的关系？

    问题3、如图(2)，△ABC∽△A′B′C′，相比为k，AD与A′D′分别是△ABC和△A′B′C′的高，试证明AD/A′D′=k的理由

    由此引出：相似三角形对应高的比等于相似比

    问题4、相似三角形对应中线、角平分线有怎样的关系？

    问题5、小结相似三角形对应线段的关系.

    问题6、填表

    　
    		 全等三角形
    		 相似三角形
    判定条件
    　
    		 　
    		 　
    性　 质
    　
    		 　
    		 　

    试题详情

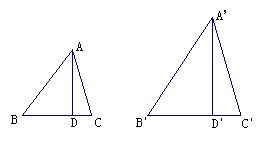
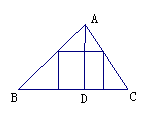    情境1：如图(1)△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是什么？

    　　　　　 图(1)　　　　　　　　 图(2)

    情境2：全等三角形的对应线段(高、中线、角平分线)有何关系？那么相似三角形的对应线段又有怎样的关系呢？

    试题详情

    1.课本P133页第4题和P134页第5题.
    2.如图：已知梯形两条边的长分别为36和60，高为32，这个梯形两腰的延长线的交点到两底的距离分别是多少？

    　

    说明：拓展练习可以在做完课本练习后根据情况选择使用.

    		　

    试题详情

    活　 动　 内 　容
    		 师生互动思考与安排
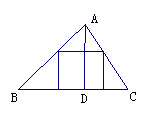    情境1：如图△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是什么？
    　
    　
    　
    　
    　
    　
    说明：对一过个情况，教者不需要有意地加以引导，只需让学生感受到解决这一问题的挑战性即可，从而激发学生探索新知的兴趣.
    情境2：全等三角形的对应线段(高、中线、角平分线)有何关系？那么相似三角形的对应线段又有怎样的关系呢？
    问题1. 全等三角形的对应线段(如高、中线、角平分线)有怎样的关系？怎样说理，选举其中一例加以说明.
    说明：问题1. 要求学生回忆全等三角形对应线段相等这一性质及说理的方法，以便为下面的说理做好铺垫.
    问题2. 相似三角形的对应边成比例，对应线段有怎样的关系？
    说明：组织学生讨论交流，激发学生思考，渗透类比
    活　 动　 内　 容
    		 　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    师生互动思考与安排
    的思想方法，让学生在已有知识的基础上，作出合理的猜想.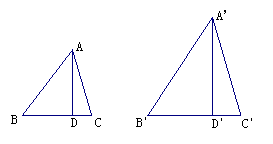
    问题3. 如图，△ABC∽△A’B’C’，相比为k，AD与A’D’分别是△ABC和△A’B’C’的高，试证明AD/A’D’=k的理由
    　
    　
    　
    　
    　
    　
    　
    说明：该过程，课本在说明“相似三角形面积的比等于相似比”的理由中已经给出，教学中，应鼓励学生通过独立思考，自主完成.
    问题4. 由刚才的说理，我们可以得出相似三角形的对应高有何关系？请加以概括.
    说明：问题4.培养学生的表达能力和善于总结的良好的学习习惯.
    问题5.相似三角形对应中线的比，对应角平分线的边有类似的性质吗？
    说明：该活动的教学要求较高，可按如下步骤进行：
    (1)引导学生根据题意，画出相应的图形，并根据图形写出题设条件；(2)鼓励学生类比刚才的说明“相似三角形对应高的比等于相似比”的说理方法，通过小组后作交流，探索结论；(3)学生结合图形，说理，在教学过程中，应让学生充分经历“操作--观察--探究--说理”的数学活动过程.以发展学生的合情推理和有条理的表达能力，另外，对于“相似三角形对应角平分线的比等于相似比的性质”，只要求学生在探索过程中，加以研究，不要求在此基础上加以运用，以控制教学的难度.
    问题6. 小结相似三角形对应线段的关系.
    问题7. 填表
    　
    		 全等三角形
    		 相似三角形
    判定条件
    　
    		 　
    		 　
    性　 质
    　
    		 　
    		 　

    		　
    活　 动　 内　 容
    		 师生互动思考与安排
    说明：问题7引导列表将判定全等三角形的条件和全等三角形的性质与判定相似三角形的条件和相似三角形的性质加以归纳、比较，利于学习形成良好的学习方法.
    		 　

    试题详情

    3、经历“操作--观察--探索--说理”的数学活动过程，发展合情推理和有条理的表达能力.

    试题详情

    2、会运用相似三角形对应高的比与相似比的性质解决有关问题；

    试题详情

    1、运用类比的思想方法，通过实践探索得出相似三角形，对应线段(高、中线、角平分线)的比等于相似比；

    试题详情


    同步练习册答案