2．探索活动

　　 活动一　 说明“相似三角形对应高的比等于相似比”的理由.

　　 课本在说明“相似三角形面积的比等于相似比”的理由中，实际上已经说明了“相似三角形对应高的比等于相似比”，基于此，课本在这里没有再给出“相似三角形对应高的比等于相似比”的说理过程．教学中，应鼓励学生通过独立思考，自主完成．

　　 活动二　 探索相似三角形对应中线的比、对应角平分线的比与相似比之间的关系．

　　 该活动的教学要求较高，表现为：(1)需要根据题意，画出相应图形，并根据图形写出题设条件；

　 (2)探索结沦；(3)说理(有条理地表达)．在教学中，应让学生充分经历“操作一观察一探索一说理”的数学活动过程，以发展学生的合情推理和有条理的表达能力．

　　 活动三　 小结、归纳．

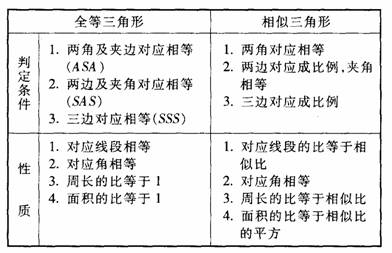在研究了相似三角形的性质之后，应引导学生列表将判定全等三角形的条件和全等三角形的性质与判定相似三角形的条件和相似三角形的性质加以归纳、比较：

　　 应强调的是：对“相似三角形对应中线的比、对应角平分线的比等于相似比”的性质，一般只要求让学生经历“操作一观察一探索一说理”的数学活动过程，加以探究，不要求在此基础上加以应用，以控制教学的难度．

1．情境创设

　　 全等三角形的对应线段(如高、中线、角平分线等)都相等．相似三角形的对应线段有怎样的关系?

2．经历“操作一观察一探索一说理”的数学活动过程，发展合情推理和有条理的表达能力．

[教学过程]

1．探索相似三角形、相似多边形的性质，会运用相似三角形、相似多边形的性质解决有关问题．

10．5　相似三角形的性质

(第二课时)

[教学目标]

4．小结

　　 (1)探索相似三角形、相似多边形的性质：相似三角形(多边形)周长的比等于相似比、面积的比等于相似比的平方，会运用相似三角形(多边形)的性质解决有关问题；

(2)经历“操作一观察一探索一说理”的数学活动过程，发展合情推理和有条理的表达能力．

3．例题教学

　　 例1是相似三角形性质：“相似三角形周长的比等于相似比、面积的比等于相似比的平方”的应用．

　　 对比例尺的概念学生已经了解，教学中应向学生说明，比例尺就是两个相似图形的相似比．

　　 对于例1学生一般不会感到困难，教学中应鼓励学生独立思考，自主练习完成．

2．探索活动

　　 活动一　 探索两个相似三角形、两个相似多边形

　 的周长之间的关系．

　　 活动分为2个层次．

　　 第一层次：引导学生根据章头图中的两个相似多边形，利用合情推理，经过操作、观察、归纳，得出两个相似多边形的周长的比等于相似比．

　　 第二层次：说明“扣似三角形周长的比等于相似比”的理由．

　　 课本利用引入比值k的方法研究相似三角形、相似多边形的性质，这不仅为后续学习奠定了基础，还渗透了一个重要的思想方法，教学中应给予说明．

　　 对“相似多边形周长的比等于相似比”性质的研究，教学中，可给出两个相似的五边形或两个相似的六边形，引导学生结合图形，通过说理来探索结论．

　　 活动二　 探索两个相似三角形、两个相似多边形的面积之间的关系．

　　 活动分为2个层次．

　　 第一层次：引导学生根据章头图中的两个相似多边形，利用合情推理，经过操作、观察、归纳，得出两个相似多边形的面积的比等于相似比的平方．

　　 第二层次：说明“相似三角形面积的比等于相似比的平方”的理由．

　　 说理过程分为3步：第一，根据题设条件说明两个直角三角形相似；第二，由两个直角三角形相似得到对应线段成比例；第三，利用三角形面积公式，推出相应结论．

　　 同“相似三角形周长的比等于相似比’’的说理过程一样，课本同样利用引入比值A的方法研究相似三角形的这一性质，教学中应给予说明．

　　 课本利用“卡通人”给出了转化的思想方法：把两个相似多边形分成若干个相似三角形．教学中，可以

　以两个五边形相似为例，引导学生理解转化的思想方法，通过独立思考和合作交流完成其说理过程．

1．情境创设

　　 (1)前面学习了相似三角形、相似多边形的概念，知道如果两个三角形或两个多边形相似，那么它们的对应角相等、对应边成比例。相似三角形、相似多边形是否还有其他的一些性质呢?这需要我们进一步探索、研究．

　　 (2)所有的正方形都是相似形(它们的对应角相等、对应边成比例)．若正方形的边长为1，则周长为 4，面积为1；若正方形的边长为2，则周长为8，面积为4；若正方形的边长为3，则周长为12，面积为9；若正方形的边长为a，则周长为4a，面积为a²．这些正方形间周长的比、面积的比与其边长的比之间有怎样的关系?

　　 (3)在本章的章头活动中，通过实际操作，知道这两个多边形相似，并且它们的相应角相等、对应边成比例，除此之外，同学们还发现了什么?