
2.知道在平行光线的照射下,不同物体的物高与影长成比例.
1.了解平行投影、中心投影、盲区的意义.
10.7 相似三角形的应用
(第一课时)
[教学目标]
6.作业:
P146 习题10.7 6、7、8.
5.小结
(1)通过具体实例,认识视点、视线和盲区;
(2)在实际应用中,进一步巩固相似三角形的有关知识.
4.练习
P144练习题: 1、2
3.探索活动
同例2一样,课本设置“尝试”活动的目的仍然是:通过实际应用进一步巩固判定三角形相似的条件及相似三角形的性质;通过具体实例,使学生进一步认识视点、视线和盲区.
本题的难度不大,关键是引导学生读懂题意,能将实际问题抽象为数学问题,并引导学生理解:问题“当小强与树AB的距离小于多少时,就不能看到树 CD的树顶D”的实质就是求图中线段FG的长.
3.通过测量活动,综合运用判定三角形相似的条件和三角形相似的性质解决问题,增强用数学的意识,加深对判定三角形相似的条件和三角形相似的性质的理解.
教学过程
 1.情境创设
1.情境创设
(1)同学们玩过“捉迷藏”的游戏吗?你认为躲藏者藏在何处,才不容易被寻找者发现?
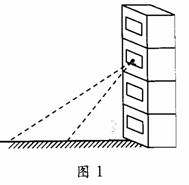
(2)如图1,小强站在3楼窗口能看到楼下的小丽吗?为什么?
你认为小丽站在什么位置时,小强才能看到她?
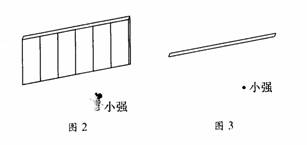
(3)如图2,小强站在一座木板墙前,小丽在墙后活动.你认为小丽应在什么区域内活动,才能不被小强看见?请在图2的俯视图图3中画出小丽的活动范围;
(4)你能举出生活中类似的例子吗?
 2.例题教学
2.例题教学
设置例2的目的是:
(1)在实际运用中,进一步巩固判定三角形相似的条件及相似三角形的性质等知识;
(2)通过具体实例,使学生了解视点、视线和盲区的概念.
在例2的解答中,“点O、C、A恰好在一条直线上,点O、D、B也恰好在一条直线上”的结论,是由实际问题:将一枚1元的硬币,放在眼睛与月球之间,调整硬币与眼睛间的距离,直到硬币刚好将月球遮住,抽象为数学结沦得出的.
(需要说明的是:本例为了得到正确的结论,题设中“硬币与眼睛的距离为2.72m”的条件不尽合理.)
解答中, 由△OCD∽△OAB,OF、OE分别是△OCD、△OAB对应边上的高,得到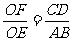 的根据是相似三角形的性质:相似三角形对应高的比等于相似比.
的根据是相似三角形的性质:相似三角形对应高的比等于相似比.
2.知道在平行光线的照射下,不同物体的物高与影长成比例.
1.通过具体实例,认识视点、视线和盲区;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com