4．小结

　　 (1)通过具体实例，认识视点、视线和盲区；

　　 (2)在实际应用中，进一步巩固相似三角形的有关知识．

3．探索活动

　　 同例2一样，课本设置“尝试”活动的目的仍然是：通过实际应用进一步巩固判定三角形相似的条件及相似三角形的性质；通过具体实例，使学生进一步认识视点、视线和盲区．

　　 本题的难度不大，关键是引导学生读懂题意，能将实际问题抽象为数学问题，并引导学生理解：问题“当小强与树AB的距离小于多少时，就不能看到树 CD的树顶D”的实质就是求图中线段FG的长．

3．通过测量活动，综合运用判定三角形相似的条件和三角形相似的性质解决问题，增强用数学的意识，加深对判定三角形相似的条件和：：：角形相似的性质的理解．

[教学过程]

　　 1．情境创设

　　 (1)同学们玩过“捉迷藏”的游戏吗?你认为躲藏者藏在何处，才不容易被寻找者发现?

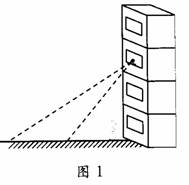
　　 (2)如图1，小强站在3楼窗口能看到楼下的小丽吗?为什么?

　　 你认为小丽站在什么位置时，小强才能看到她?

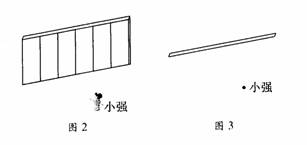
　　 (3)如图2，小强站在一座木板墙前，小丽在墙后活动．你认为小丽应在什么区域内活动，才能不被小强看见?请在图2的俯视图图3中画出小丽的活动范围；

　　 (4)你能举出生活中类似的例子吗?

　　 2．例题教学

　　 设置例2的目的是：

　　 (1)在实际运用中，进一步巩固判定三角形相似的条件及相似三角形的性质等知识；

　　 (2)通过具体实例，使学生了解视点、视线和盲区的概念．

　　 在例2的解答中，“点O、C、A恰好在一条直线上，点O、D、B也恰好在一条直线上”的结论，是由实际问题：将一枚1元的硬币，放在眼睛与月球之间，调整硬币与眼睛间的距离，直到硬币刚好将月球遮住，抽象为数学结沦得出的．

　　 (需要说明的是：本例为了得到正确的结论，题设中“硬币与眼睛的距离为2.72m”的条件不尽合理．)

　　 解答中，　 由△OCD∽△OAB，OF、OE分别是△OCD、△OAB对应边上的高，得到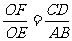的根据是相似三角形的性质：相似三角形对应高的比等于相似比．

2．知道在平行光线的照射下，不同物体的物高与影长成比例．

1．了解平行投影、中心投影、盲区的意义．

10．7　相似三角形的应用

(第三课时)

[教学目标]

3．小结

　　 (1)了解平行投影的含义；

　　 (2)通过观察、测量等操作活动，探究在平行光线的照射下，物体的物高与影长的关系，并解决有关的实际问题．

2．探索活动

　　 活动一　 试验探究，得出结论．

　　 活动分为3个层次．

　　 第-层次：试验探究．

　　 引导学生根据已有的生活经验，感悟到：在阳光下，在同一时刻，物体的高度与物体的影长存在某种关系：物体的高度越高，物体的影长就越长，并在此基础上组织探究试验．

　　 对试验探究活动的教学要注意两点：

　　 (1)各小组通过观察、测量、计算出的结果存在着一定的误差，在引导学生探究结论时，一般应取各小组测量结果的平均值；

　　 (2)教学中，各小组的测量是在同一时刻进行的，其他时刻情况如何?学生可能存在疑问，对此可在教学中向学生展示教师事先在其他几个不同时刻测量出的结果，再次引导学生探究．

　　 第二层次：了解平行投影．

　　 第三层次：引导学生归纳出：在平行光线的照射下，不同物体的物高与影长成比例．

　　 活动二　 组织尝试活动．

　　 图10-27是-幅立体图形，学生根据“太阳光线可以看成平行光线”的表述画出与图中虚线平行的线段-般不会感到困难．教学中，要引导学生通过观察、分析，感悟到画乙、丙两根木杆的影长(用线段表示)时，它们应与甲木杆在阳光下的影长平行．

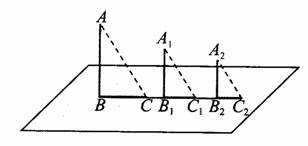图中的太阳光线、木杆及其影子构成了3个直角三角形，但它们不在同一平面内．如果将这3个直角三角形平移到同一平面内，可以得到如图的图形：

　　 引导学生思考：如何用三角形相似的知识说明在乎行光线的照射下，不同物体的物高与影长成比例．

　　 活动三　 应用举例．

　　 课本列举古埃及测量金字塔的问题作为相应知识的应用．该问题对学生来说有一定的难度，教学时建议做如下铺垫：

　　 (1)铺垫练习：如，在阳光下，身高1.68m的小强在地面上的影长为2m，在同一时刻，测得旗杆在地面上的影长为18m．求旗杆的高度(精确到0.1m)．

　　 (2)作变式：如果要求测量的是一个等腰三角形的高，你将如何计算?

　　 (3)较充分地展开图10-28中立体图形转化为平面图形的过程．

1．情境创设

　　 (1)当人们在阳光下行走时，会出现--个怎样的现象?(学生思考片刻，回答是影子)

　　 光线在直线传播过程中，遇到不透明的物体，在这个物体的后面光线不能到达的区域便产生影．

　　 你能举出生活中的例子吗?

3．通过测量活动，综合运用判定三角形相似的条件和三角形相似的性质解决问题，增强用数学的意识，加深对判定三角形相似的条件和：：：角形相似的性质的理解．

[教学过程]