1.下列关于判断一个数学结论是否正确的叙述正确的是( )
A.只需观察得出 B.只需依靠经验获得
C.通过亲自实验得出 D.必须进行有根据地推理.
11.1 你的判断对吗
[新知导读]
图中的两条线段AB与CD哪一条长一些？先猜一猜，再量一量.
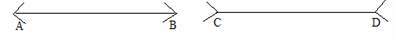
[范例点睛]
如图11-1-1，假如用一根比地球赤道长1 m的铁丝将地球赤道围起来，那么铁丝与地球赤道之间的间隙能有多大(把地球看成球形)？能放进一颗红枣吗？能放进一个拳头吗？与同伴进行交流.
图11-1-1
思路点拨：要判断一个数学结论是否正确，仅仅依靠经验、观察或实验是不够的，必须一步一步、有根有据地进行推理.
[课外链接]
费马数猜想：大师的失误
1640年，在数论领域留下不可磨灭足迹的费马思考了一个问题：式子 +1 的值是否一定为素数。当
n取0、1、2、3、4时，这个式子对应值分别为3、5、17、257、65537，费马发现这五个数都是素数。由此，费马提出一个猜想：形如 +1的数一定为素数。在给朋友的一封信中，费马写道：“我已经发现形如 +1的数永远为素数。很久以前我就向分析学家们指出了这个结论是正确的。”费马同时坦白承认，他自己未能找到一个完全的证明。费马所研究的 +1这种具有美妙形式的数，后人称之为费马数，并用Fn 表示。费马当时的猜想相当于说：所有费马数都一定是素数。费马是正确的吗？
进一步验证费马的猜想并不容易。因为随着n的增大， Fn 迅速增大。比如对后人来说第一个需要检验的F5＝4294967297已经是一个十位数了。非常可能的是，由于这一数太大，所以费马在得出自己的猜想时并没有对它进行验证。那么，它到底是否如同费马所相信的那样是一个素数呢？
1729年12月1日，哥德巴赫(哥德巴赫猜想的提出者)在写给欧拉的一封信中问道：“费马认为所有形如 +1的数都是素数，你知道这个问题吗？他说他没能作出证明。据我所知，也没有其他任何人对这个问题作出过证明。”
这个问题吸引了欧拉。1732年，年仅25岁的欧拉在费马死后67年得出F5 ＝641×6700417，其中641=5×27+1这一结果意味着
是一个合数，因此费马的猜想是错的。
在对费马数的研究上，费马这位伟大的数论天才过分看重自己的直觉，轻率地做出了他一生唯一一次错误猜测。更为不幸的是，研究的进展表明费马不但是错的，而且非常可能是大错特错了
[随堂演练]
|
活 动 内 容 |
师生互动思考与安排 |
|
1.下列关于判断一个数学结论是否正确的叙述正确的是( ) A.只需观察得出 B.只需依靠经验获得 C.通过亲自实验得出 D.必须进行有根据地推理. 2.通过观察你能肯定的是( ) A.图形中线段是否相等; B.图形中线段是否平行 C.图形中线段是否相交; D.图形中线段是否垂直 3．有一正方体，将它各面上分别标出a、b、c、d、e、f.有甲、乙、丙三个同学站在不同角度观察结果如图，问这个正方体各个面上的字母的对面各是什么字母，即a的对面为 ，b的对面为 ，c的对面为 . 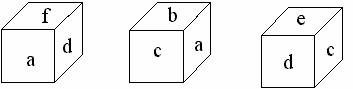 4.春节联欢晚会,某班组委会组织了一个有趣的活动,两个人握一次手,若每两人握手一次,则全班56个人共握几次手?n个人共握多少次手呢? 5.地理老师在黑板上画了一幅世界五大洲的图形，并给每个洲都写上了代号，然后，他 请5个同学每人认出2个大洲来，5个同学的回答是： 甲：3号是欧洲，2号是美洲； 乙：4号是亚洲，2号是大洋洲； 丙：1号是亚洲，5号是非洲； 丁：4号码是非洲，3号是大洋洲； 戊：2号码是欧洲，5号是美洲； 地理老师说：“你们每个人都认对了一半”，请问，每个号码各代表什么洲呢？ |
|
|
活 动 内 容 |
师生互动思考与安排 |
如图⑴是一张8㎝×8㎝的正方形纸片，把它剪成4块，按图⑵所示重新拼合.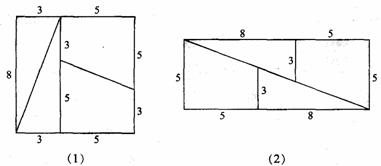 这4块纸片恰好能拼成一个长为13，宽为5的长方形吗？试试看，并与全班同学交流. 说明：本例题应主要让学生自己通过分组合作共同研究，判断能否完成这样的拼图，进一步感受到仅凭观察、猜想、操作、实验是不够的，强调我们在以后的数学学习中要学会说理. |
|
2．如图，两个大小相同的大圆，其中一个大圆内有10个小圆，另一个大圆内有2个小圆，你认为大圆内的10个小圆的周长之和与另一个大圆内的2个小圆的周长之和哪一个大一些？请你猜一猜，并用学过的知识和数学方法验证你的猜想.
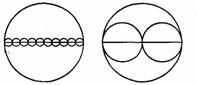
说明：这两个情景教学实例，告诉我们数学中观察、猜想有时不一定正确，引导学生运用已有的知识和方法进行验证它的正确性，进
一步培养学生数学思考的严密性和合理性.
|
活 动 内 容 |
师生互动思考与安排 |
||
|
情景1 观察、思考和实验是人类发现、发明、创造的发端。我们曾通过观察、操作、实验等探索活动，发现了许多正确的结论. 难道所有的探索活动获得的结论都是正确的吗？ 如图，从一只透明的空玻璃杯的侧面能看到杯子下面放了一枚硬币. ⑴如果向杯中注水，猜一猜这时从杯子的侧面还能看到这枚硬币吗？ ⑵试一试，你看到了硬币吗？
情景2 装有半杯水的透明玻璃杯中，插入一根笔直的筷子，这时我们会看到什么结论呢？ 答：进入水里的部分被弯折了并且变大了.
探索活动 1. 如图，两条线段AB与CD那一条 长一些？先猜一猜，再量一量. 3．在交流中，感受数学思考的合理性和严密性；从而培养学生在生活、学习等过程中处理问题应认真分析，有理有据，切勿跟着感觉走,养成以理服人的良好品质. 2．让学生初步体验证明说理的方法和重要性. 1. 让学生经历一些观察、操作活动，并对获得的数学猜想进行实验验证，体验直观判断有时不一定正确，从而尝试从数学的角度运用所学的知识和方法寻求证据、给出证明. 本节课是命题说理证明的预备课，起着承上启下的作用。故本节课的教学主要通过学生身边熟悉的一些情景实例,让学生自己发现我们在观察事物和分析评价时不能仅仅靠直觉观察，应该有严密的推理证明。通过玻璃杯实验、线段的长短比较以及正方形拼图等等，发现仅靠观察、实验得到的结论不一定正确。 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com版权声明：本站所有文章，图片来源于网络，著作权及版权归原作者所有，转载无意侵犯版权，如有侵权，请作者速来函告知，我们将尽快处理，联系qq：3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |
说明：情景1、2学生亲身经历这两个实验的全过程,体验到生活中有时会产生错觉；事实上，在数学中有时也会产生错觉.