
根据上述教材结构与内容分析,考虑到学生已有的认知结构心理特征 ,制定如下教学目标:
1 基础知识目标:理解定义、命题、真命题、假命题、定理的含义,会区分命题的条件(题设)和结论,奠定推理论证的基础.
2 能力训练目标:
在交流中发展有条理思考和有条理表达的能力。
《说理2》是初中数学新新课程八年级第十一章第二节的第2课时。在此之前,学生已学习了《 你的判断对吗》和说理第1课时,本课时主要是对定义、命题进行研究,为学习数学说理打下理论基础。
6.如图,AB是圆O的直径,把AB分成几条相等的线段,分别以每条线段为直径画小圆.设AB=a,那么圆O的周长L=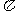 a.
a.
计算:(1)把AB分成2条相等的线段,每个小圆的周长L2=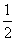
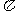 a=
a=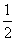 L;
L;
(2)把AB分成3条相等的线段,每个小圆的周长L3=________;
(3)把AB分成4条相等的线段,每个小圆的周长L4=________.
……
(4)把AB分成n条相等的线段,每个小圆的周长Ln=________.

结论:把大圆的直径分成n条相等的线段,分别以每条线段为直径画小圆,那么每个小圆的周长是大圆周长的________.
请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系.
[后花园]
妙趣角 小明和小芳所在的年级有4个班,每班都有正、副班长各一人,这8人中没有2人是同姓的.平时召开年级的班长会议时,各班都只派1名班长参加.参加第一次会议的是小杨、小童、小方、小刘;参加第二次会议的是小叶、小童、小汪、小刘;参加第三次会议的是小杨、小叶、小童、小徐.3次会议小金都因病没有参加.请问每个班各是哪两位班长?
为了解决这个问题,我们可以按如下的方法进行思考:
(1)先把参加会议的情况列表如下:
|
|
小杨 |
小童 |
小方 |
小刘 |
小叶 |
小汪 |
小徐 |
小金 |
|
第一次会议 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
第二次会议 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
|
第三次会议 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
(2)依据表格进行推理.由题意可知,两人同班的必要条件是他们没有一次会议是同时出席的.按照这个条件,从上表中首先可以发现,3次会议都出席的小童与3次会议都没有出席的小金同班;然后从出席两次会议的小杨、小刘、小叶出发,不难从表中找到小杨与小汪同班,小刘与小徐同班,小叶与小方同班.
推理时,利用表格来帮助思考是一种非常有效的方法.
5.小明和小亮两人合作玩一个扑克牌游戏,规则如下:
小明背对小亮,让小亮按下列4个步骤操作:
第一步 分发左、中、右三堆牌,每堆牌不少于两张,且各堆牌现有的张数相同;
第二步 从左边一堆拿出两张,放入中间一堆;
第三步 从右边一堆拿出一张,放入中间一堆;
第四步 左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆.
这时,小明准确地说出了中间一堆牌现有的张数.你认为中间一堆牌现有的张数是_________.小明是如何获得结果的?
4.甲、乙、丙3倍同学中有一位做了一件好事.李老师问他们:“谁做了好事?”他们“调皮”地说了下面几句话:
甲说:“我没有做这件事,乙也没有做这件事.”
乙说:“我没有做这件事,丙也没有做这件事.”
丙说:“我没有做这件事,也不知谁做了这件事.”
当李老师追问时,他们承认上面每人讲的话中都有一句真话,一句假话.根据这些条件,你能分析出到底是谁做了好事吗?
[拓展与延伸]
3.(1)如图①,一块三角尺XYZ放置在△ABC上,三角尺的两条直角边XY、XZ恰好分别经过点B、C.△ABC中,∠A=30°,则∠ABC+∠ACB=_____°,∠XBC+∠XCB=____°.
(2)如图②,设∠A=a,改变三角尺XYZ的位置,但两条直角边XY、XZ仍然分别经过点B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请说明理由;若不变化,请求出∠ABX+∠ACX的大小.

① ②
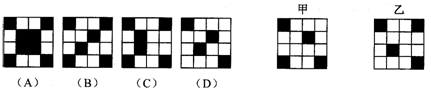
2.平移图形甲,使它与图形乙重叠,形成的图形是( ).
1.根据左图大方格里上、下、左、右四个数之间的关系,你认为右图的空白方格中应填什么数?为什么?

2.进一步认识和体会说理的必要性.
[基础与巩固]
1.能在观察、实验、操作的基础上,对所作的猜想进行说理.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com