
4.在交流中发展有条理思考和有条理表达的能力.
[教学过程(第一课时)]
3.了解定义、命题、真命题、假命题的含义,会区分命题的条件和结论.
2.尝试用说理的方法解决问题,体验说理必须步步有据.
1.经历探索一些问题时,由于“直观判断不可靠”、“直观无法做出确定判断”,但运用已有的数学知识和方法可以确定一个数学结论的正确性的过程,初步感受说理的必要性.
11.2 说理
[教学目标]
4.小结
(1)说说你对命题的认识;
(2)举出1-2个命题,并分别说出它们的条件和结论.
3.例题教学
课本没有安排例题,教学时可将本节“讨论”的问题作为例题进行教学.
2.探索活动
问题一 (1)什么是总体的一个“样本”?
(2)怎样的两个数叫“互为相反数”?
(3)怎样的两个图形叫“全等形”?
设计问题一,学生回忆这些概念的定义,引导学生感受数学中如何给概念下定义;;’
定义的规则是:(1)应相等,即定义概念和定义概念的外延相等;(2)不应循环;(3)一般不应是否定判断;(4)应清楚确切.
教学中只要通过具体的例子来引导学生感受就可以了.
问题二 (1)“等角的余角相等.”与“等角的余角相等吗?”这两句话一样吗?如不一样,它们有什么不同?
(2)“经过一点有且只有一条直线与已知直线垂直”与“经过一点画已知直线的垂线”有什么不同?
(3)“四边形不是多边形”与“四边形不一定是多边形”又有什么不同?
问题二中的句子,一类是对某一件事情做出了判断;另一类是没有对某一件事情做出判断.引导学生通过这两类(命题与非命题)具体例子的辨析,了解什么是命题,什么不是命题.
对某一件事情做出判断的句子,有的做出了正确的判断,有的做出了错误的判断。比如,“四边形不是多边形”这个句子的判断是错误的,教学中学生可能会误认为这样的句子不是命题.可以结合这个例子,说明凡做出判断的句子都是命题,不论判断是否正确.
问题三 请你例举一些命题.
问题四 观察下列命题,你能发现它们有什么共同的结构特征吗?
命题(1)如果a>0,b<0,那么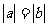
命题(2)如果两个三角形的三条边对应相等,那么这两个三角形全等;
命题(3)如果一个三角形有2个角相等,那么这 2个角所对的边也相等.
问题五 下列各命题的条件是什么?结论是什么?
命题(4)对顶角相等;
命题(5)同位角相等,两直线平行;
命题(6)面积相等的两个三角形全等.
由于命题“对顶角相等”的条件和结论不明显,学生可能会把这个命题分成“对顶角”和“相等”两部分,认为这个命题的条件是“对顶角”,这个命题的结论是“相等”.实际教学中,可以在学生讨论、交流的基础上,画出与这个命题相关的图形,于是就有不同的表述(这个命题的条件是“两个角是对顶角”,结论是“这两个角相等”),对照图形比较这两种不同的表述.前一种的表述中,条件和结论都不是完整的句子,显然不如后一种的表述清楚准确.进而引导学生对于条件
和结论不明显的命题可以先画出与命题相关的图形或将命题改写成“如果……那么……”的形式,然后再写出条件和结论.
问题六 在上述6千命题中,哪些命题做出的判断是正确的?哪些命题做出的判断是错误的?你是如何知道它们做出的判断是错误的?
命题(2)、(3)、(4)、(5)是真命题,命题(1)、(6)是假命题.教学中,应在学生充分交流各自的判断方法的基础上,引导学生体会:①真命题:如果题设成立,那么判断总是正确的;假命题:当题设成立时,判断不能保证总是正确的.②要说明一个命题是假命题,只要举出一个“反例”就可以了;而要说明一个命题是真命题,无论验证多少个例子,都无法保证这个命题的正确性.关于“反例”,将在本章第4节再做介绍,这里初步引导学生体会反例的作用.
1.情境创设
日常生活中,人们为了交流思想,常常用到一些名称和术语,只有对这些名称和术语有了共识,才可以正常的交流.类似地,数学中要进行说理,必须对涉及的概念有共识,也就是需要对概念下定义.
3.小结
(1)说说你对“说理”的感受;
(2)本节课我们不仅用举例的方法来说明一个数学结论是错误的;而且我们用“说理”的方法来确认一个数学结论的正确性.从而使我们能更全面地、深入地认识一些数学现象。
[教学过程(第二课时)]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com