
1.2005年冬季,新七十二名泉评选结果揭晓,济南市所辖的五个区中皆有名泉分布,小明由此推断济南市历城区一定有名泉。他的这个推理 (填“正确”或“不正确”)
11.2 说理(1)
[新知导读]
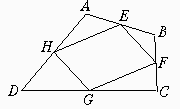
如图:四边形ABCD四边的中点分别为E、F、G、H.度量四边形EFGH的边和角,你会发现什么结论?
[范例点睛]
例1.某参观团依据下列约束条件,从A、B、C、D、E五个地方选定参观地点:
(1) 如果去A地,那么也必须去B地;
(2) D、E两地至少去一处;
(3) B、C两地只去一处;
(4) C、D两地都去或都不去;
(5) 如果去E地,那么A、D两地也必须去
依据上述条件,你认为参观团只能去__________________
思路点拨:由(2)知,D、E两地至少去一地,若去E地,则由(5)也必须去A、D地,于是由于(1)和(4)必须去B、、C两地,但与(3)矛盾,所以不能去E地,因此必须去D地。由(4)也必须去C地,再由(3)知,不能去B地,从而由(1)知也不能去A地,故参观团只能去C、D两地。
例2.如图,已知∠AOB=90°,OM是∠AOB平分线,按以下要求解答问题:
将三角板的直角顶点P在射线OM上移动,两直角边分别与边OA、OB交于C、D
(1) 在甲图中试说明PC=PD
(2)
在乙图中点G是CD与OP交点,且PG=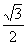 PD求△POD与△PDG的面积之比
PD求△POD与△PDG的面积之比
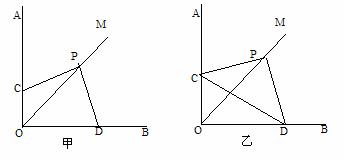
思路点拨:(1)过P点分别向OA、OB边作垂线段PE、PF,由角平分线的性质得PE=PF,从而△PCE≌△PDF,所以PC=PD;(2)由PC=PD可知∠PDC=∠POD=45°,则△PDG∽△POD,所以△POD与△PDG的面积之比为对应边之比的平方。
[课外链接]
有一栋居民住宅楼,每两层之间的楼梯都是由17级台阶组成的,一位初中学生一口气从一楼一级台阶一级台阶地跑到最高一层,紧接着又一级台阶一级台阶地回到一楼,他一边跑一边数自己的脚由一级台阶移到另一级台阶的次数,当他数到238时,恰好回到一楼,试问:这是一栋多少层的楼房?
[随堂演练]
4.小结
(1)说说你对命题的认识;
(2)举出1-2个命题,并分别说出它们的条件和结论.
3.例题教学
课本没有安排例题,教学时可将本节“讨论”的问题作为例题进行教学.
2.探索活动
问题一 (1)什么是总体的一个“样本”?
(2)怎样的两个数叫“互为相反数”?
(3)怎样的两个图形叫“全等形”?
设计问题一,学生回忆这些概念的定义,引导学生感受数学中如何给概念下定义;;’
定义的规则是:(1)应相等,即定义概念和定义概念的外延相等;(2)不应循环;(3)一般不应是否定判断;(4)应清楚确切.
教学中只要通过具体的例子来引导学生感受就可以了.
问题二 (1)“等角的余角相等.”与“等角的余角相等吗?”这两句话一样吗?如不一样,它们有什么不同?
(2)“经过一点有且只有一条直线与已知直线垂直”与“经过一点画已知直线的垂线”有什么不同?
(3)“四边形不是多边形”与“四边形不一定是多边形”又有什么不同?
问题二中的句子,一类是对某一件事情做出了判断;另一类是没有对某一件事情做出判断.引导学生通过这两类(命题与非命题)具体例子的辨析,了解什么是命题,什么不是命题.
对某一件事情做出判断的句子,有的做出了正确的判断,有的做出了错误的判断。比如,“四边形不是多边形”这个句子的判断是错误的,教学中学生可能会误认为这样的句子不是命题.可以结合这个例子,说明凡做出判断的句子都是命题,不论判断是否正确.
问题三 请你例举一些命题.
问题四 观察下列命题,你能发现它们有什么共同的结构特征吗?
命题(1)如果a>0,b<0,那么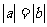
命题(2)如果两个三角形的三条边对应相等,那么这两个三角形全等;
命题(3)如果一个三角形有2个角相等,那么这 2个角所对的边也相等.
问题五 下列各命题的条件是什么?结论是什么?
命题(4)对顶角相等;
命题(5)同位角相等,两直线平行;
命题(6)面积相等的两个三角形全等.
由于命题“对顶角相等”的条件和结论不明显,学生可能会把这个命题分成“对顶角”和“相等”两部分,认为这个命题的条件是“对顶角”,这个命题的结论是“相等”.实际教学中,可以在学生讨论、交流的基础上,画出与这个命题相关的图形,于是就有不同的表述(这个命题的条件是“两个角是对顶角”,结论是“这两个角相等”),对照图形比较这两种不同的表述.前一种的表述中,条件和结论都不是完整的句子,显然不如后一种的表述清楚准确.进而引导学生对于条件
和结论不明显的命题可以先画出与命题相关的图形或将命题改写成“如果……那么……”的形式,然后再写出条件和结论.
问题六 在上述6千命题中,哪些命题做出的判断是正确的?哪些命题做出的判断是错误的?你是如何知道它们做出的判断是错误的?
命题(2)、(3)、(4)、(5)是真命题,命题(1)、(6)是假命题.教学中,应在学生充分交流各自的判断方法的基础上,引导学生体会:①真命题:如果题设成立,那么判断总是正确的;假命题:当题设成立时,判断不能保证总是正确的.②要说明一个命题是假命题,只要举出一个“反例”就可以了;而要说明一个命题是真命题,无论验证多少个例子,都无法保证这个命题的正确性.关于“反例”,将在本章第4节再做介绍,这里初步引导学生体会反例的作用.
1.情境创设
日常生活中,人们为了交流思想,常常用到一些名称和术语,只有对这些名称和术语有了共识,才可以正常的交流.类似地,数学中要进行说理,必须对涉及的概念有共识,也就是需要对概念下定义.
11.2说理(2)教案
[教学过程]
3.小结
(1)说说你对“说理”的感受;
(2)本节课我们不仅用举例的方法来说明一个数学结论是错误的;而且我们用“说理”的方法来确认一个数学结论的正确性.从而使我们能更全面地、深入地认识一些数学现象.
2.探索活动
问题一 七年级某班的学生通过多次计算代数式 的值,得到了以下的一些结论:
的值,得到了以下的一些结论:
(1)无论x取什么数,代数式 的值总是偶数;
的值总是偶数;
(2)无论x取什么数,代数式 的值总是正数;
的值总是正数;
(3)无论x取什么数,代数式 的值不是负数;
的值不是负数;
(4)无论x取什么数,代数式 的值大于1.
的值大于1.
你认为这些结论是否正确?
实际教学中,对于结论(1)、(4),学生容易发现当x=1时,这个代数式的值为1,不是偶数,从而说明这两个结论是错误的.设计判断结论(1)、(4)真、假性的活动,实质是初步引导学生感受利用反例可以说明一个命题是错误的.
问题二 你能确认问题一中的结论(2)、(3)是正确的吗?
实际教学中,在判断问题一的结论(2)、(3)的真假性时,学生各自通过一些计算代数式 的值后,既有强力的确认结论真、假性的欲望,又有不可能无穷地计算代数式的值的无奈.营造这样的教学氛围,以利于引导学生借助已有的知识和方法来说理,从而再一次感受“说理”的必要性以及“说理”是确认一个数学结论正确性的有力工具.
的值后,既有强力的确认结论真、假性的欲望,又有不可能无穷地计算代数式的值的无奈.营造这样的教学氛围,以利于引导学生借助已有的知识和方法来说理,从而再一次感受“说理”的必要性以及“说理”是确认一个数学结论正确性的有力工具.
问题三 通过本节数学实验室的探索活动,对你探索得到的结论有什么看法?
由于学生已有通过观察、度量、猜想所得到的结论有时不一定可靠的体验,以及初步感受到“说理”是确认一个数学结论正确性的有力工具,因此学生对本节数学实验室探索得到的结论就有如何“说理”的需求,虽然学生暂时不能解决,但这个悬念促使学生向往、追求着“说理”.
1.情境创设
课本以“图11-6中的一条直道、一条曲径占用草坪的面积相等吗?”作为本节的问题情境,由于学生在探索这个问题时,直观无法做出确定的判断,因此可以在学生广泛交流不同意见的过程中引导他们主动地进行“说理”,从而感受“说理”是确定一个数学结论正确性的有力工具.
实际教学中,学生可能会有以下的想法:①因为小路曲曲弯弯,比直路长,而且处处1m宽,所以曲路的面积比直路的面积大;②作长方形草坪一边的垂线,可以把小路割补成长方形,所以直路的面积与曲路的面积相等;③换一个角度计算小路的面积--通过计算草坪的面积就知道了小路的面积等.
教学中还可以选用学生有兴趣的素材,以利于学
生感受说理的必要性.例如:
(1)水结成冰时,体积增加了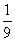 ,冰化成水时,体积减少了几分之几?
,冰化成水时,体积减少了几分之几?
(2)如果用一根很长的钢缆沿赤道绕地球1圈,然后把钢缆放长10m,你想象一下,这时钢缆与地球赤道之间的缝隙有多大?你估计可以通过一头牛,还是一只老鼠?
(3)从小明、小丽多次进行60m赛跑中,发现小明比小丽先到达终点,而且小明到达终点时小丽总是还离终点10m.如果小明在起点处后退10m,两人同时出发,他们能同时到达终点吗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com