
2、 如图:四边形ABCD≌四边形A′B′C′D′,∠A=∠A′,∠B=∠B′,∠C=∠C′,另外一组对应角是______,对应边是____、____、____、____。
1、 当两个相似图形的相似比K=___时,这两个图形是全等的。
我们知道:要判断两个图形是否全等,只要看它们能否重合。对于全等多边形,我们知道:全等多边形的对应边、对应角分别相等.这就是全等多边形的特征.实际上这也是我们识别全等多边形的方法,即如果两个多边形的_______________________________________________________________________________那么这两个多边形全等.
如图3所示,如果两个五边形的边、角分别对应相等,那么这两个五边形全等.
例5: AB= A′B′,BC= B′C′,CD= C′D′,DE= D′E′,AE= D′E′,
∠A= ∠A′,∠B =∠B′,∠C =∠ C′,∠D = ∠D′,∠E =∠E′,
根据所有边、角分别 的两个多边形全等
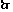 五边形
≌五边形
五边形
≌五边形
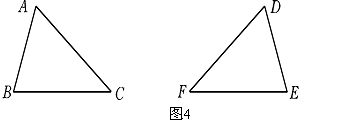
如图.4所示,如果两个三角形的边、角分别对应相等,那么这两个三角形全等
例6: AB= A′B′,BC= B′C′,AC= A′C′,
AB= A′B′,BC= B′C′,AC= A′C′,
∠A= ∠A′,∠B =∠B′,∠C =∠C′,
根据所有边、角分别 的两个三角形全等
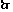 △
≌△
△
≌△
上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过运动而重合,相互重合的顶点叫做 顶点,相互重合的边叫做 ,相互重合的角叫做 .根据重合,我们知道:全等多边形的对应边、对应角分别相等.这就是全等多边形的特征.

如图3中的两个五边形是全等的,记作五边形ABCDE ≌五边形A′B′C′D′E′.(这里,符号“≌”表示全等,读作“全等于”)其中AB与 是对应线段,BC与 是对应线段,CD与 是对应线段,DE与 是对应线段, AE与 是对应线段。∠A与 是对应角,∠B与 是对应角,∠C与 是对应角, ∠D与 是对应角, ∠E与 是对应角。
例1:五边形ABCDE≌五边形A′B′C′D′E′
根据全等多边形的 分别相等
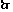 AB= ,BC= ,CD= ,DE= ,AE= ,
AB= ,BC= ,CD= ,DE= ,AE= ,
∠A= ,∠B = ,∠C = ,∠D = ,∠E = ,
例2:图3中,(1)若AE=2cm,则A′E′= cm
(2)若∠A=∠E=∠D=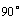 ,∠B=
,∠B=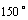 ,则∠A′=
,则∠A′=  ,∠C′=
,∠C′= 
如图.4所示,△ABC与△DEF.全等,记作
其中:AB与 是对应线段,DF与 是对应线段,BC与 是对应线段。
∠A与 是对应角,∠E与 是对应角,∠C与 是对应角。
例3:  △ABC≌△DEF
△ABC≌△DEF
根据全等三角形的 分别相等
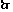 AB= ,BC= ,CD= ,
AB= ,BC= ,CD= ,
∠A= ,∠B = ,∠C = ,
例4:图3中,(1)若△ABC的周长为17 cm,BC=6 cm,DE=5 cm,则DF = cm
(2)若∠A
=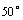 ,∠E=
,∠E=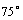 ,则∠B=
,则∠B= 
观察图.1中的平面图形,判断有没有两个图形的大小和形状是完全相同的?有什么方法?

能够完全 的两个图形就是全等图形。
图中的________和________就是全等图形.
在日常生活中,处处可以看到全等的图形.例如:同一张底片印出的同样尺寸的照片;我们使用的数学课本的封面;我们班的课桌面等等,请试着尽可能多地举出生活中全等图形的例子,比一比,看谁举出的例子多.
思 考(多种方法)
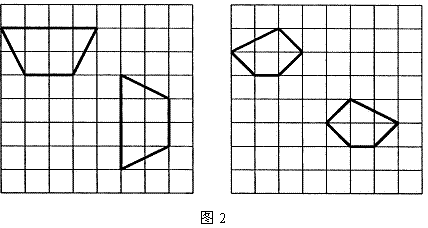
观察图2中的两对多边形,其中的一个可以经过怎样的运动和另一个图形重合?
学习目标:理解全等图形和全等多边形的概念,理解全等多边形的对应边、对应角相等。
学习重、难点:理解全等多边形的对应边、对应角相等
学生看出图片,翻折、旋转、平移是4种变化-----------引出
学习过程:
4、你能从等边三角形出发,设计一个漂亮的图案吗?试试看。
3、下列图案是由若干个全等图形拼成的。请你找出这个全等的图形并画出来,再仿此自己设计一个美丽的图案。
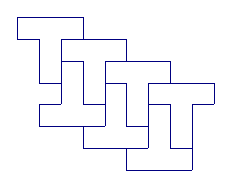
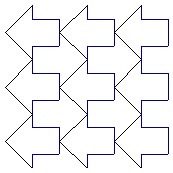
2、利用如左图所示的基本图形,在右图方格中设计图案。
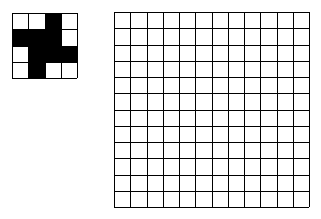
1、按下列步骤设计图案:
(1)画出两个小长方形,如下图(1)。
(2)分别把每个小长方形的一半涂黑,如下图(2)。
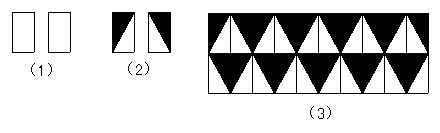 (3)再做出若干个这样的图案,利用它们拼出一个美丽的图案,如下图(3)。
(3)再做出若干个这样的图案,利用它们拼出一个美丽的图案,如下图(3)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com