
(四)作业
教材第90页习题第1、2题.
(三)小结
(1)全等图形、全等多边形、全等三角形的概念.
(2)全等多边形的性质与识别方法;全等三角形的性质.
(二)新课
由前面的讲述知:能完全重合的两个图形就是全等图形.
由此,刚才方格纸中的就是全等图形.
下面,我们看看图形的运动对全等图形有何影响?
活动 请同学们在方格纸中任意画一个多边形,先将这个多边形沿某一方向平移一定距离(与原图形无重叠);再将原多边形绕形外一点顺时针(或逆时针)旋转一定角度(与原图形无重叠);然后将原图形沿形外某格线对称;最后将这些图形剪下来,将其叠合.你能发现什么?通过这个活动过程,说明了什么问题?
发现叠合时,几个图形能完全重合.
说明图形经过平移、旋转、翻折的图形运动,位置发生了变化,但形状和大小却没有改变,图形运动前后的两个图形是全等的;反过来,也就是说,两个全等的图形经过图形运动一定能重合.
我们学习了相似多边形,由刚才的活动,请你说说什么是全等多边形?什么是全等多边形的对应顶点、对应角、对应边?你认为全等多边形有何特征?
全等多边形对应边、对应角分别相等.
如图1,四边形ABCD与四边形EFGH全等,可记为四边形ABCD≌四边形?EFGH,请指出对应顶点、对应角、对应边.
实际上,满足这一特征的两个多边形全等.
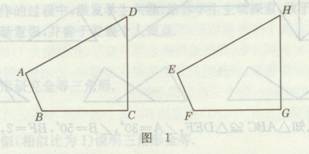
全等多边形的识别方法:如果两个多边形对应边、对应角分别相等,那么这两个多边形全等.
三角形是特殊的多边形,所以,全等三角形的对应边、对应角分别相等;如果两个三角形的对应边、对应角分别相等,那么这两个多边形全等.
如△ABC与△EFG全等,可记为△ABC≌△EFG.
例1 如图2,已知将△ABC绕其顶点A顺时针方向旋转20°后得到△ADE.

(1)△ABC与△ADE的关系如何?
(2)求∠BAD的度数.
分析:将△ABC绕其顶点A旋转得到△ADE,故△ADE是由△ABC旋转得到的,若将△ADE逆时针方向旋转20°,则能与△ABC重合,所以△ABC与△ADE是全等的.
由学生自主思考、分析解答.
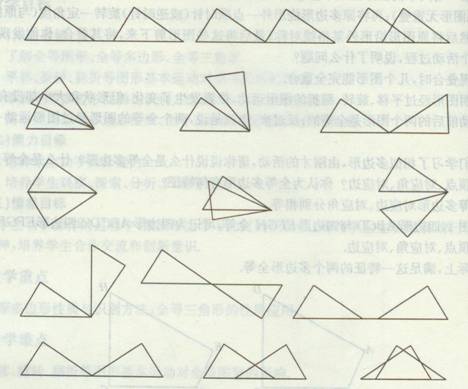
探索:请同学们将两张纸叠起来,剪下两个全等三角形,然后将叠合的两个三角形纸片放在桌面上,从平移、旋转、对称几个方面进行摆放,看看两个三角形有一些怎样的特殊位置关系?并画出这些位置关系的代表性图形.
请小组同学合作、讨论、交流.(下面是部分代表性结论)
例2 如图3,已知△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,求∠DFE的度数和EC的长.

分析:由三角形的内角和求出∠ACB,再由△ABC≌△DEF,知△ABC和△DEF的对应边相等,对应角相等,从而求出∠DFE的度数和EC的长.
解:因为 ∠ACB=180°-∠A-∠B
=180°-30°-50°=100°,
又因为 △ABC≌△DEF,
所以 ∠DFE=∠ACB=100°,
EF=BC,
所以 EC=EF-CF=BC-CF=BF=2,
即∠DFE的度数为100°,EC的长为2.
(一)引入
我们已经学习过相似图形,那么相似图形有何特征和性质?相似多边形呢?相似三角形呢?当相似比k=1时,相似图形有何特殊性?
下面,我们具体的学习图形的全等.
问题:请观察方格纸中所画的平面图形(编出序号),找出其中的相似图形(图略).
在你所找出的相似图形中,有些图形不仅形状相同,而且大小也一样,你发现了吗?你能用什么方法来判断两个图形形状和大小相同?
显然,将两个图形叠合,看是否完全重合.
多媒体,实物展示台,剪刀,方格纸.
引导法,探究法,演示法,类比法,讨论交流法.
平移、旋转、翻折等图形基本运动对全等图形的影响.
全等多边形性质与识别方法;全等三角形的性质应用.
(三)情感目标
在学生动手操作的过程中,激发学生学习几何的积极性,培养学生主动探索,敢于实践的科学精神,培养学生合作交流和创新意识.
(二)能力目标
1.培养学生动手操作能力.
2.培养学生观察、探索、分析、归纳等能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com