
2.如果“两角及一边”条件中的边是其中一角的对边。
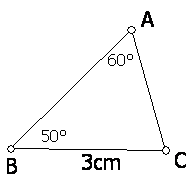
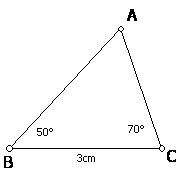
例如下图,在△ABC中,∠A=60°,∠B=50°,BC=3cm,你能画出一个三角形,使它的两个内角分别是60°和50°,而且60°所对的边为3cm吗?你画的三角形与△ABC全等吗?
(提示:这里的条件与1中的条件有什么相同点与不同点?你能将它转化为1中的条件吗?)
议一议:
改变△ABC中相应的角度和边长,你能得到同样的结论吗?
于是我们又得到两个判定两个三角形全等的方法:
两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。
两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”。
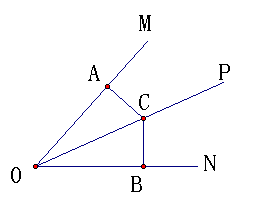
例题1:如图,OP是∠MON的角平分线,C是OP上一点,CA⊥OM,CB⊥ON,垂足分别为A、B,△AOC≌△BOC吗?为什么?
练习:第142页第1、2、3题
议一议:(略)
小结:
本节课我们又学习了判定两个三角形全等的两种方法“角边角”和“角角边”,这样连“边角边”我们一共学习了三种判定两个三角形全等的方法了。同学们在应用这些方法解决问题时,要具体问题具体分析,找出正确的途径。
教学素材:
A组题:
1.如图,B点是线段EF的中点,BA=BC,AE=CF。△ABE和△CBF全等吗?说说你的理由。

如图5-5-4,AB=DF,AC=DE,BE=CF。你能找到一对全等三角形吗?说明你的理由。

B组题:
你还记得怎样用尺规作一个角等于已知角吗?你能说明其中的道理吗?
小明回顾了作图的过程,并进行了如下的思考:


OC=O C
C ,OD=O
,OD=O D
D ,CD=C
,CD=C D
D
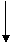
△OCD≌△O C
C D
D
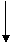
∠DOC=∠D O
O C
C
你能说明每一步的理由吗?
2、填空:
(1) 如图,已知AO=DO,∠AOB与∠DOC是对顶角,还需补充条件___________=_____________,就可根据“SAS”说明△AOB≌△DOC;
(2)
 如图,已知∠AOB与∠DOC是对顶角,还需补充条件____________=_____________,____________=_____________,就可说明△AOB≌△DOC。
如图,已知∠AOB与∠DOC是对顶角,还需补充条件____________=_____________,____________=_____________,就可说明△AOB≌△DOC。
B组题:
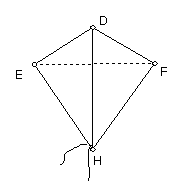
小明做了如图所示的风筝,其中∠EDH=∠FDH,ED=FD,将上述条件标注在图中,小明不用测量就能知道EH=FH。你知道为什么吗?


(2)试用一条直线将所给的长方形分成两个全等三角形,有多少种分法?你发现了什么结论?

B组题:
1、分别找出各题中的全等三角形,并说明理由。



|
2.填空
如图,已知AO=DO,∠AOB与∠DOC是对顶角,还需补充条件______________=_______________,就可根据“ASA”说明△AOB≌△DOC;或者补充条件_______________=_______________,就可根据“AAS”,说明△AOB≌△DOC。(若把“AO=DO”去掉,答案又会有怎样的变化呢?)

B组题:
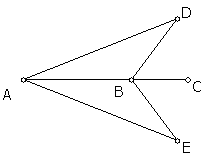 如图,一艘轮船沿AC方向航行,已知轮船在A点测得航线两侧的灯塔与航线的夹角相等,当轮船到达B点时测得这两个灯塔与航线的夹角仍然相等,这时轮船与两个灯塔的距离是否相等,为什么?
如图,一艘轮船沿AC方向航行,已知轮船在A点测得航线两侧的灯塔与航线的夹角相等,当轮船到达B点时测得这两个灯塔与航线的夹角仍然相等,这时轮船与两个灯塔的距离是否相等,为什么?

新课讲解:
同学们会说这需要量一下这个三角形的边长和内角的度数,那么请问:你准备量哪几条边长,哪几个内角的度数?能尽量少吗?
我们一起来分析:
只知道一个条件(一条边或一个角)画三角形,能保证画出的三角形与△ABC全等吗?
知道两个条件画三角形,有几种可能的情况?(两条边或两个角或一条边和一个角)
每种情况下作出的三角形一定与△ABC全等吗?我们来试一次。
量得△ABC中,BC=3cm,∠B=50°,画画看。
还是不行,当然如果我们只知道△ABC中其它两个条件,例如只知道两个角的度数,也还是不能保证作出的三角形与△ABC全等。有兴趣的话可以课后试试。
如果知道三个条件画三角形,你能说出有哪几种可能的情况?
(有四种可能:三条边、三个角、两边一角和两角一边)
做一做:
在△ABC中,已知∠A=70°,∠B=50°,∠C=60°,你能画出一个与△ABC全等的三角形吗?
(不能,因此三个内角对应相等的两个三角形不一定全等)
在△ABC中,已知AB=2.8cm,∠A=70°,AC=2.5cm,你能画出一个与△ABC全等的三角形吗?
 两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”。
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”。
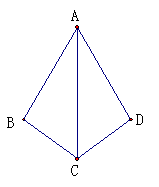
例题1:例1:如图,AB=AD,
∠BAC=∠DAC,请问:△ABC
和 △ADC是否全等?为什么?
练习:第139页第1、2题
小结:本节课我们通过操作实践,发现了判定两个三角形全等的第一个方法--边角边。在解决实际问题时,特别在说明两个三角形全等的理由时,应根据已知条件及图形中的有关条件,依照“SAS”加以说明。
教学素材:
A组题:
1.分别找出各题中的全等三角形,并说明理由。

2.如果“两角及一边”条件中的边是其中一角的对边。
例如下图,在△ABC中,∠A=60°,∠B=50°,BC=3cm,你能画出一个三角形,使它的两个内角分别是60°和50°,而且60°所对的边为3cm吗?你画的三角形与△ABC全等吗?
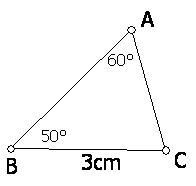
(提示:这里的条件与1中的条件有什么相同点与不同点?你能将它转化为1中的条件吗?)
议一议:
改变△ABC中相应的角度和边长,你能得到同样的结论吗?
于是我们又得到两个判定两个三角形全等的方法:
两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。
两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”。
例题1:如图,OP是∠MON的角平分线,C是OP上一点,CA⊥OM,CB⊥ON,垂足分别为A、B,△AOC≌△BOC吗?为什么?
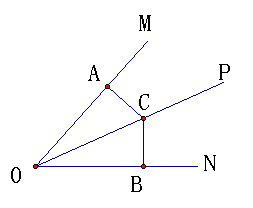
练习:第142页第1、2、3题
议一议:(略)
小结:
本节课我们又学习了判定两个三角形全等的两种方法“角边角”和“角角边”,这样连“边角边”我们一共学习了三种判定两个三角形全等的方法了。同学们在应用这些方法解决问题时,要具体问题具体分析,找出正确的途径。
教学素材:
A组题:
2、填空:
(1) 如图,已知AO=DO,∠AOB与∠DOC是对顶角,还需补充条件___________=_____________,就可根据“SAS”说明△AOB≌△DOC;
(2)
 如图,已知∠AOB与∠DOC是对顶角,还需补充条件____________=_____________,____________=_____________,就可说明△AOB≌△DOC。
如图,已知∠AOB与∠DOC是对顶角,还需补充条件____________=_____________,____________=_____________,就可说明△AOB≌△DOC。
B组题:
小明做了如图所示的风筝,其中∠EDH=∠FDH,ED=FD,将上述条件标注在图中,小明不用测量就能知道EH=FH。你知道为什么吗?
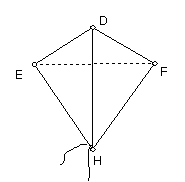


(2)试用一条直线将所给的长方形分成两个全等三角形,有多少种分法?你发现了什么结论?

B组题:
1、分别找出各题中的全等三角形,并说明理由。



|
11.3 探索三角形全等的条件
|
教学目标 |
知识目标:(1)掌握SSS、SAS、ASA、AAS及HL使用方法; (2)初步领会几何问题分析方法; (3)能灵活地应用三角形全等的条件解决具体问题. 情感目标:(1)通过学生合作交流,增进学生之间的感情交流; (2)经历探索过程,感受成功喜悦,提高学习兴趣. |
||||
|
教材分析 |
地位与作用:“三角形全等的判定”是后续学习必备的能力,也是学生形成分析、探究能力起点. 重 点:“三角形全等的条件”的应用,通过合作交流,探索几何解题的方法及解题过程的表述. 难 点:灵活地应用三角形全等的条件,学会常见问题的分析、常用方法的归纳. |
||||
|
教学准备 |
投影仪及相关胶片 |
||||
|
教 学 过 程 |
|||||
|
教师活动 |
学生活动 |
设计意图 |
|||
|
一、创设情境导入新课 1、提出问题: (1)我们已经学习了探索三角形全等的条件这一节内容,请大家思考一下判定三角形全等的方法有几种,分别是什么? (2)如果你们家中的三角形窗户上的玻璃坏了,想请个木工师傅帮你重新划一块,你需要向木工师傅提供哪些数据,木工才能根据你提供的数据为你划一块合适的玻璃? (从生活实际出发,启发学生应用所学知识解决实际问题) |
学生回答 (1)一般三角形有四种;直角三角形有五种. 分别为:SSS,SAS,ASA,AAS;HL (2)三条边长、两边长及夹角的度数,两角度数及所夹边的长度,两角度数及其中一角对边的长度,如果是直角三角形中还有斜边与直角边的长度. |
由于学生所学判定方法是分五节课学习,五种判定方法间的联系与区别用得比较少,综合应用能力较差,在课前应做这方面的准备. 由判定方法到实际应用,进一步理解全等三角形的条件; 联系实际,便于应用和深刻理解. |
|||
二、问题探讨 问题1:给出四组图形,判断其中全等的三角形有哪些,说明理由.. 问题1:给出四组图形,判断其中全等的三角形有哪些,说明理由..找一找,然后与同桌交流; |
生答: (1)与(5)、(2)与(7) (3)与(8)、(4)与(6) 理由:(四个同学说) |
投影仪给出问题 留有时间让学生去发现,并思考为什么?巩固学生对全等三角形的认识和感受,形式多种,有利于学生综合应用能力的提高. |
|||
|
问题2:已知,如图△ABC与△DEF,B、E、C、F四点在一条直线上,根据下列各题所给出的条件,解决相关的问题: (1)若已知BC=EF,∠B=∠DEF,则还需增加条件 ,可判定△ABC≌△DEF? (2)若只知道BC=EF,则还需添加两个什么条件,可判定△ABC≌△DEF; (3)若除了题干中所给的条件以外,没有其它任何条件,让你给出判定△ABC≌△DEF的条件,应该如何加条件? 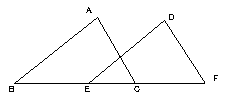 变式:若把题中的图形变为下图所示,其它不变,以上各题该如何解?  你还有更好的变式方法吗?讲出来,与大家分享一下. 你还有更好的变式方法吗?讲出来,与大家分享一下.
|
(1)可添加角等的条件: ∠A=∠D或∠ACB=∠F; 也可添加边等的条件:AB=DE. (2)可以从有一组边对应相等的判定方法中找,发现有SSS SAS ASA AAS可用,因而有四种方式可填;1+2+1+2=6种. (3)内容比前面两种方式更广,可以判定的根据不同来分,如:SSS只有一种;SAS有3种可能;AAS有6种不同情况;ASA有3种. 说明:以上主要是针对直接使用三角形全等的判定方法来找的;实际上本题还可以进一步挖掘,如AB与DE平行等.  变式后:具体的找法还一样,只不过有点变化. 变式后:具体的找法还一样,只不过有点变化.分享:
|
本题主要目的是逐步引导学生去探索三角形全等的方法的使用,培养学生从多角度去认识图形,利用不同方法来思考应用.提高学生的灵活应用能力.同时通过本题渗透分类思想的应用. 变式的主要目的是使学生能够通过做题,把具有共同特征和类似方法的问题联系在一起,经过归纳总结,形成系统的知识,达到举一反三的目的. 充分让学生去思考和讨论,让学生感受成功的喜悦,培养数学学习的兴趣. |
|||
|
做一做 如图,已知AB=BD,∠ABC= ∠DBC,AC与BD相等吗?为什么? 若保持A、B、D点位置不变,∠ABC=∠DBC,当BC的长度改变时,AC与CD相等吗?为什么?  在此过程中有一些特殊的位置,可以组成特殊的图形,有哪些结论成立? |
让学生先做,然后提问,学生补充完善,形成结论. 如: 角平分线上的点到角两边的距离相等; 等腰三角形顶角的平分线,也是底边上的高,还是底边上的中线; |
引导学生不仅要会做题,同时还要发现规律,重视特殊结论的总结和应用. |
|||
问题3 如图, 已知∠ACB=90°,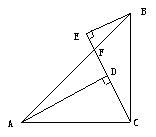 AC=BC,BE⊥CE,AD⊥CE,垂足 AC=BC,BE⊥CE,AD⊥CE,垂足分别为E、D,图中线段CE与AD是否相等?并说明理由. 师:安排学生讨论,引导学生分析. 图中还有其它相等的线段吗? 若有请写出来. 你还能发现一些相关线段的关系吗?  变式:若本题的图如下图所示,其它条件不变,AD和CE还相等吗?为什么? 变式:若本题的图如下图所示,其它条件不变,AD和CE还相等吗?为什么? |
学生讨论后回答; 直观观察:发现相等; 如何说明? 三角形全等 全等的条件是什么? ASA或AAS 说明不是用HL 有, BE=CD AD-BE=DE 变式:相等,方法同上. 小结:两个图形在文字的叙述上是相同的,但图形是不同的,可思考的方式方法是相类似的,学的时候要重视方法的归纳和应用. |
引导学生如何去探求解题的方法和途径,先感知结果,然后加以验证. 学会应用性质,探索更多的结论,开拓视野. 让学生从对比中发现两题之间的联系,感受分析方法的共同之处,从中获得启发.形成解决问题能力. |
|||
 做一做 如图,AB=AC,AD=AE,∠BAC=∠DAE,BE与CD相等吗?为什么? 做一做 如图,AB=AC,AD=AE,∠BAC=∠DAE,BE与CD相等吗?为什么?老师引导学生讨论、分析 可适当延伸:图不变,现要使BE=CD,还可以,把条件变换为已知 , , . |
学生合作讨论 谈分析的思路,及补充发言,而后写解题过程. |
让学生能够感受几何问题的多变性和灵活性,学会利用所学知识灵活解决问题,达到练习巩固的目的. |
|||
|
二、小结回顾 本课你有哪些收获?从知识、方法和感受方面说. |
(1)掌握三角形的全等条件的应用方法;能够正确地使用它去说理. (2)感受几何图形的能力增强,同时还进一步地理解了一些特殊的结论. |
知识系统化、规律化,便于学生的掌握和应用. |
|||
|
三、巩固作业 1.个人独立完成作业:随堂练习; 2.小组合作完成作业: 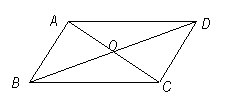 如图,四边形ABCD中,对角线AC、BD相交于点O,且OA=OC,OB=OD;请问,图中共有几对全等的三角形,它们分别是什么?为什么? 如图,四边形ABCD中,对角线AC、BD相交于点O,且OA=OC,OB=OD;请问,图中共有几对全等的三角形,它们分别是什么?为什么? |
学生课后完成 |
多方位,多角度地对学生学习的知识进行应用练习,达到巩固知识,发展能力的目的. |
|||
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com