
3. 感受数学的严谨性,结论的确定性,初步养成言之有理,落笔有据的推理习惯,发展初步的演绎推理能力;
2. 能从“同位角相等,两直线平行”“两直线平行,同位角相等”这两个基本事实出发,证明平行线的判定定理和平行线的性质定理,并能简单应用这些结论;
1. 了解证明的基本步骤和书写格式;
3.小结
(1)我们通过添加辅助线,把三角形的3个内角拼成1个平角;把三角形的3个内角拼成两平行线的同旁内角,证明了三角形内角和定理及推论,从中可以体会到,不同的添加辅助线方法的实质是相同的--把一个我们不会解的新问题,转化为我们会解的问题;
(2)从基本事实出发证实了曾探索得到有关平行线的结论的正确性、三角形内角和定理及推论,由此还可以继续证明一个又一个定理:
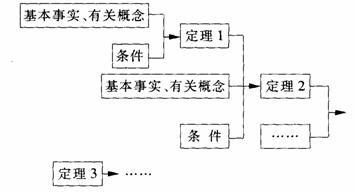
2.探索活动
问题一 如何证明三角形内角和等于180°?你有没有困惑?
问题二 你有没有办法在平面图形中把三角形的三个内角“搬”到一起?
添加辅助线,实质是构造新图形.由于学生没有接触过辅助线,实际教学中学生可能采用的方法有:
(1)拼图中把一个角移动位置的活动,通过画一个角等于这个角来实现;
(2)从已有的对图形的平移、旋转的认识出发,通过角的平移、旋转把三角形的3个内角“搬”到一起.
教学中应引导学生根据自己的理解充分发表意见,倡导学生富有个性地采用不同的策略解决问题,然后主动发现不同的方法都可以用添加一条平行线解决.
问题三 你能说说小明的证明思路吗?
问题四 请你说说小丽的证明思路,并完成证明.
问题五 你还有不同的证明方法吗?与同学交流.
问题六 尝试证明三角形的外角与三角形的内角的大小关系.
探索活动中,不仅要关注学生能否形式化的表达,同时要更多地关注发展学生合乎逻辑的思考、步步有据地、有条理地用自己的语言表达的能力,鼓励学生主动地表达和交流.引导学生不仅从已知条件向结论探索(如本节第二课时探索活动问题二中的思路1),而且从结论向已知条件探索(如本节第二课时问题二中的思路2),或者从已知条件和结论两个方面互相逼近.
1.情景创设
三角形3个内角的和是多少?
你是如何知道的?
你认为这个结论正确吗?为什么?
设计问题情境,实质是借助拼图实践,为定理的证明铺垫了基本思路--把3个角“搬”到一起,利用平角的定义来证明,同时使添加辅助线有必要、有意义.由于学生经历了“直观判断不可靠”、“直观无法做出确定的判断”,所以实际教学中,学生会认为对三角形3个内角和结论的正确性需要确认.
4.小结
(1)回顾我们这两节课的数学活动,你有哪些收获?
(2)这两节课我们初步体验了数学证明的思路,并从基本事实出发证明得到了有关平行线的定理等.依据基本事实你还能证明哪些熟悉的结论?
[教学过程(第三课时)]
3.例题教学
本节课课本没有编排例题,教学中可以根据学生的实际情况,将证明“两直线平行,同旁内角互补”作为例题,或将课本练习第1题作为例题,引导学生尝试用多种方法来思考.比如课本练习第1题:
思考方法一:
c//d→∠3+∠5=180°→∠1+∠2=180°→∠2=130°
思考方法二:
∠3+∠4=180°→∠1+∠2=180°→∠2=130°
通过多种思考方法的交流,促使学生发散思考,并在交流中,发展学生的合乎逻辑的思考、有条理的表达的能力.
2.探索活动
问题一 与同学合作,根据“两直线平行,内错角相等”画出相关的图形,并根据所画图形写出已知、求证.
问题二 说说你的证明思路.
实际教学中,教师可以在学生充分交流的基础上再小结不同的思路:
如图11-11.
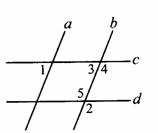 (1)已知AB//CD,可知∠3=∠2.
(1)已知AB//CD,可知∠3=∠2.
∠3与∠1是对顶角,可知∠3=∠1.
由∠3=∠2,∠3=∠1,可知∠1=∠2.
(2)要证∠1=∠2,需证∠1=∠3,∠2=∠3.
由于∠1与∠3是对顶角,所以它们相等.
要证∠2=∠3,需有AB//CD.
以利于学生不断体会推理的思考方法.
问题三 请你完成证明,并交流.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com