1．情境创设

　　 (1)我们曾探索。发现了有关平行线的哪些结论?

　　 (2)我们是如何证明“同旁内角互补，两直线平行”的?

　　 (3)从基本事实“两直线平行，同位角相等”可以证明哪些结论?

　　 设计问题情境，引导学生回顾平行线的判定及性质，主动地区别这些互逆命题；回顾平行线判定定理的证明，引导学生不断感受几何演绎体系的思维方法，并通过新问题的思考和讨论，以利于学生主动地参与本节课的教学活动．

11.3　证　明(2)

[教学过程]

4．小结

　　 证明，可以证实我们曾探索得到的许多结论的正确性．从证明中，我们可以感受到人类对真理的执着追求和严谨的科学态度．欧几里得的方法不仅对数学，而且对其他科学乃至人类的思想都产生了巨大的推动作用．请你查阅并收集这方面的有关资料．

3。例题教学

　　 例题教学中应关注：

　　 (1)引导学生体会推理的思考方法。

　　 比如：依据基本事实“同位角相等，两直线平行”．

　　 要证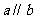，需要∠3＝∠2；要证∠3＝∠2，需要∠3＝∠1，∠2＝∠1；由于∠3与∠1是对顶角，所以它们相等；已知∠1与∠2相等，所以就可以有根有据的推理．

　　 又如：

　　 由∠1与∠3是对顶角，可知(∠1＝∠3)；由已知∠1＝∠2及已证∠1＝∠3，可知(∠2＝∠3)；由∠2＝∠3，可知()．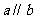

　　 (2)组织学生讨论如何有条理地表达推理过程．在充分的交流中，引导学生从开始学习证明就意识到，证明不仅要步步有据，而且证明的依据必须是基本事实、有关概念的定义、已经证明的定理及已知条件，从中感受数学的严谨．

2．探索活动

　　 问题一　 如何用推理的方法证实“同角的补角相等”的正确性呢?

　　 (1)这个命题的条件是什么?结论是什么?

　　 (2)你能根据命题的条件画出相应的图形吗?

　　 (3)要证明图11-9中的上2与上3相等，就需要知道它们有什么联系?你能说说它们之间的联系吗?

　　 设计第(3)小题的讨论，实质是引导学生逐步体会推理的思考方法，在讨论、交流中发展学生有条理的表达能力，然后教师示范推理的书写的格式．由于这个命题的证明是学生进入证明阶段的开始，所以这里有所侧重地先介绍推理的书写格式，在本节的例题中再介绍证明与图形有关的命题的一般步骤．

　　 问题二　 如何证明“对顶角相等”?

　　 可以仿照问题一中的3个小问题开展教学活动，并由学生合作完成推理过程的书写．

1．情境创设

　　 一个数学结论的正确性如何确认呢?

　　 其实数学家们早就遇到了这样的问题，人类对数学命题进行证明的研究已有两千多年的历史了．公元前3世纪，古希腊数学家欧几里得写出了举世闻名的巨著《原本》，在这本书中，他挑选了一些基本定义和基本事实作为证实其他命题的出发点，推导出400多条定理．《原本》是人类智慧的伟大成就之一，它对科学和人类文化的发展产生了深远的影响．

　　 让我们尝试从基本事实出发，证实我们曾探索、发现的有关图形的许多性质的正确性!

4．感受欧几里得的演绎体系对数学发展和人类文明的价值．

[教学过程(第一课时)]

3．感受数学的严谨、结论的确定，初步养成言之有理、落笔有据的推理习惯，发展初步的演绎推理能力．

2．能从“同位角相等，两直线平行”、“两直线平行，同位角相等”这两个基本事实出发，证明平行线的判定定理、平行线的性质定理、三角形内角和定理以及三角形内角和定理的推论，并能简单应用这些结论．

1．了解证明的基本步骤和书写格式．