
|
1.已知:如图,∠BAD=∠DCB,∠1=∠3. 求证:AD∥BC. 2.证明:同角的余角相等. 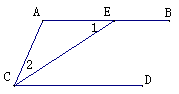 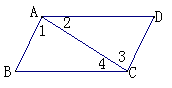 3.已知:如图,∠1=∠2,CE平分∠ACD. 3.已知:如图,∠1=∠2,CE平分∠ACD.求证:AB∥CD. |
|
|
例1、如何证明“对顶角相等” (1)仿照问题1提问 师生共同合作完成推理: 已知:如图直线AB、CD相交于点O. 求证:∠1=∠2.  证明:∵AB、CD相交于点O(已知), 证明:∵AB、CD相交于点O(已知),∴∠1+∠BOD=180°, ∴∠1=180°-∠BOD, ∠2+∠BOD=180°, ∠2=180°-∠BOD, ∴∠1=∠2(等量代换). 师生共同讨论交流: 证明与图形有关的命题,一般有哪几个步骤? (1)根据命题,画出图形; (2)根据命题,结合图形,写出已知、求证; (3)写出证明过程. 说明:1.组织学生讨论、交流,让学生自已认识如何有条理地表达推理过程. 2.在充分的交流中,引导学生从开始学习证明就意识到,证明不仅要步步有据,而且证明的依据必须是基本事实.有关概念的定义,已经证明的定理及已知条件,从中感受教学的严谨性. 3.这里教师要注意切不可讲解,可以让学生先思考,让学生表述,对于出现不规范的书写及非因及果等问题,教师要耐心引导. 例2证明:内错角相等,两直线平行. 已知:如图,直线a、b被直线C所截,∠1=∠2. 求证a∥b. 证明:∵∠1=∠2(已知), ∠1=∠3(对顶角相等). ∴∠2=∠3(等量代换), ∴a∥b(同位角相等,两直线平行). 定理:内错角相等,两直线平行. 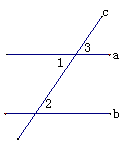 尝试:证明“同旁内角互补,两直线平行”. 尝试:证明“同旁内角互补,两直线平行”.说明:1.前面已经证实了“对顶角相等”这个性质,所以根据此性质设计证明“内错角相等,两直线平行”这个定理的证明,学生还是比较容易接受的. 2.“尝试”的证明,让学生充分发挥自已的知识积淀,从而对证明的格式有更深的理解.这里也与前面一样要让学生有条理地表述“三段论”. 3.再次感受到人类对真理的执着追求和严谨的科学态度. |
|
4. 感受欧几里得的演绎体系对数学发展和人类文明的价值.
3. 感受数学的严谨性,结论的确定性,初步养成言之有理,落笔有据的推理习惯,发展初步的演绎推理能力;
2. 能从“同位角相等,两直线平行”“两直线平行,同位角相等”这两个基本事实出发,证明平行线的判定定理和平行线的性质定理,并能简单应用这些结论;
1. 了解证明的基本步骤和书写格式;
4、证明:同角的余角相等。
3、已知:如图,∠1=∠2,CE平分∠ACD,
求证:AB∥CD.
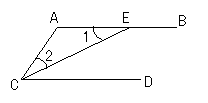 证明:
证明:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com