练习册

  • 练习册
  • 试题
     0  202445  202453  202459  202463  202469  202471  202475  202481  202483  202489  202495  202499  202501  202505  202511  202513  202519  202523  202525  202529  202531  202535  202537  202539  202540  202541  202543  202544  202545  202547  202549  202553  202555  202559  202561  202565  202571  202573  202579  202583  202585  202589  202595  202601  202603  202609  202613  202615  202621  202625  202631  202639  447090 

    1.三角形的一个外角等于和它不相邻的两个内角的和；

    试题详情

    3、　 价值观：感受欧几里得的演绎体系对数学发展和人类文明的价值。

    教学重点：能从基本事实出发证实曾探索得到的三角形内角和定理及推论的结论的正确性，并能简单应用这些结论；

    教学难点：辅助线的的添加；

    教具准备：多媒体课件。

    教学过程：

    　
    		 教学过程
    		 设计说明
    创设问题情境
    		 师：我们在七年级曾经把一个三角形的三个内角撕下来拼在一起得到一个平角，由此得到“三角形的内角和是180°”的结论。但这只是实验得出的命题，不能当做定理，只有经过严格的推理证明，证明命题的正确性，才能作为几何定理，今后，在几何里，常采用这种方法得到新知识。
    那么如何证明此命题是真命题呢？
    		 　
    从学生已有的知识引入符合学生的认知规律，且小学已知三角形三个内角和是180°。
    学生自主探究
    		 学生回忆证明一个命题的步骤：
    ①根据命题，画出图形；
    ②分析命题，根据所画图形写出已知、求证；把文字语言转化为几何语言。
    ③分析、探究证明方法。
    		 　
    有本章前面几节作为基础，学生有能力画图，写已知，求证。
    　
    创设问题情境
    		 教师引导：要证三角形三个内角和是180°，观察图形，你有没有办法利用以前的知识通过严格的推理来证明呢？同学们试试看。
    学生可能采用的方法有：
    (1)拼图中把一个角移动位置的活动，通过画一个角等于这个角来实现；
    (2)从已有的对图形的平移、旋转的认识出发。通过角的平移、旋转把三角形的3个内角“搬”到一起。
    　
    		 联想前面撕角拼角的方法，学生能想到。
    　　 让学生体会转化的数学思想方法，把新知识化为旧知识。
    　
    　
    　
    　
    　
    　
    　
    学生自主探究
    		 学生通过自主探究，可以得出以下几种辅助线的作法：
    ①　　 如图1，延长BC得到一平角∠BCD，然后以CA为一边，在△ABC的外部画∠1=∠A。　　　　　　　　　　　　
    ②　　 如图1，延长BC，过C作CE∥AB
    ③　　 如图2，过A作DE∥AB　　　　　　　　　　
    ④　　 如图3，过C作CD∥AB。
    ⑤如图4，在BC边上任取一点P，作PD∥AB，PE∥AC。
    学生可能还有其它画法。

    		 　
    　
    　
    　
    学生通过观察分析、归纳，使思维达到高潮，由感受性认识上升到理性认识。
    请不同画法的学生板演，并口述画图方法，叙述不恰当时，同学可改正，
    画法4，部分学生可能想到。
    辨析与研讨
    		 通过以上分析、研究，让不同做法的学生讲解依据。
    ①　　 根据平行线的判定及性质，利用同位角把三角形三内角转化为一个平角。
    ②　　 根据平行线的性质，利用内错角和同位角，把三角形三内角转化为一个平角。
    ③　　 根据平行线的性质，利用内错角，把三角形三内角转化为一个平角。
    ④　　 根据平行线的性质，利用内错角把三角形三内角转化为两平行线间的同旁内角。
    ⑤　　 根据平行线的性质，利用内错角、同位角或同旁内角把三角形三内角转化为一个平角。
    　
    		 进一步搞清作辅助线的思路和合乎逻辑的分析方法，充分让学生表述自己的观点，这个过程对培养学生的能力极为重要，依据不充分，学生可争论。
    　
    学生自主探究
    		 　
    　
    根据以上几种辅助线的作法，选择一种,师生合作，写出示范性证明过程。其余由学生自主完成证明过程。
    　
    　
    　
    　
    		 　　
    　
    目的是培养学生的思维能力和推理能力。
    　
    反思与
    评价
    		 1、　 弄清证明命题的必要性及步骤。
    2、　 如何将文字语言转化为几何语言。
    3、　 三角形内角和定理的证明是借助于什么获得(实验、观察、添加辅平行线)，平行线是以后几何中常作的辅助线。
    4、　 添辅助线的技巧：通过平行线把三角形三个内角转化为平角或两平行线间的同旁内角，即把新知识转化为旧知识去解决。
    		 　
    引导学生进行总结和概括，培养学生的归纳概括能力。
    思考
    		 如图，∠是△ABC的一个外角，∠与△ABC的内角有怎样的大小关系？
    由三角形内角和定理，可以知道：∠=∠A+∠B，

    　

    三角形内角和定理的推论：

    试题详情

    2、　 情感与态度目标：培养学生热爱数学，对数学浓厚的学习兴趣，顽强的学习毅力，独立思考、勇于创新的学习精神，形成良好的个性品质。

    试题详情

    1、　 知识与能力目标：能从基本事实出发证实曾探索得到的三角形内角和定理及推论的结论的正确性，并能简单应用这些结论；感受数学的严谨、结论的确定，初步养成言之有理、落笔有据的推理习惯，发展初步的演绎推理能力；

    试题详情

    11.3证明(3)

    教学内容：教材第172-173

    教学目标：理解并掌握三角形的内角和是180°。依据这一节课标的要求，结合八年级学生的认知水平、年龄特征和学生实际情况等确立本节课教学的目标为：

    试题详情

    1.如图1，AB∥CD，
    (1)∠A、∠P、∠C三角之间存在怎样的关系？用两种方法证明你的结论.
    (2)如果将P点向右移，如图2， AB∥CD，此时∠A、∠P、∠C三角之间存在怎样的关系？并证明你的结论.
    　
    　
    　
    　
    　
    　
    　
    2.如图，△ABC中，AB=AC，
    求证∠B=∠C.
    　
    　
    　
    　
    3.求证：六边形的内角和为720°.
    		 　

    试题详情

    例：如图，梯形ABCD中，AD∥BC，∠B=∠C，求证：梯形ABCD是等腰梯形.
    分析：为了将∠B、∠C“搬”到
    一个三角形，可过点D作DE∥AB交
    BC于E，从而∠1=∠B，又因∠B=
    ∠C，所以∠1=∠C，故DE=DC，又由
    于AD∥BC，易知四边形ABED是平行
    四边形，从而DE=AB，因此AB=CD，根据“两腰相等的梯形是等腰梯形”.
    1. 请同学们根据分析，完成证明过程并与同学交流.
    2. 你还有不同的证明方法吗？
    说明：一般来说，梯形问题都可转化为三角形和平行四边形问题，为此平移一腰或延长梯形的两腰或分别过上底的两个顶点，向梯形的下底作高.让学生体会数学中转化思想，即把不熟悉的转化为熟悉的.
    		 　

    试题详情

    2. 三角形的一个外角大于任何一个和它不相邻的内角.

    说明：这里用多种方法来证明三角形内角和定理，让学生更能体会到证明这种逻辑推理思维.同时各种探索活动使学生能形式化的表达，发展学生合乎逻辑的思考、步步有据地、有条理地用自已的语言表达并鼓励学生主动地表达与交流，引导学生不仅从已知条件向结论探索，而且从结论向已知条件探索或从已知条件和结论两个方面互相逼近.

    		 　

    试题详情

    活动内容
    		 师生互动思考与安排
    问题一：
    1.三角形3个内角的和是多少？
    2.你是如何知道的？
    3.你认为这个结论正确吗？你有过怀疑吗？为什么？
    说明：设计问题情境，实质是借助拼图实践，为定理的证明铺垫了基本思路--把3个角“搬”到一起，利用平角的定义来证明，同时使添加辅助线有必要、有意义，由于学生经历了“直观判断不可靠”、“直观无法做出确定的判断”，所以实际教学中，学生对三角形3个内角和结论的正确性需要确认，也就是证明.
    问题二：
    1.如何证明三角形内角和等于180°？
    2.你有没有办法在平面图形中把三角形的三个内角“搬”到一起？
    分析：添加辅助线，实质是构造新图形，由于学生没有接触过辅助线，实际教学中学生可能采用的方法有：
    (1)拼图中把一个角移动位置的活动，通过画一个角等于这个角来实现.
    (2)从已有的对图形的平移、旋转的认识出发，通过角的平移、旋转把三角形的3个内角“搬”到一起.
    3.你能想办法把∠A、∠B“搬”到相应的位置上吗？
    已知：△ABC.
    求证：∠A+∠B+∠C=180°.
    证明：如图，作BC的延长线CD，过点C作CE∥AB,
    ∵CE∥AB,
    ∴∠1=∠B(两直线平行，同位角相等),
    ∴∠2=∠A(两直线平行，内错角相等).
    ∵∠1+∠2+∠ACB=180°(平角的定义),
    ∴∠A+∠B+∠ACB=180°(等量代换).

    　
    　
    　
    　
    　
    通过证明我们现在对三角形内角和等于180°不再产生怀疑了，于是得到：
    三角形内角和定理：三角形三个内角的和等于180°.
    说明：证明后可以让让学生知道三角形定理的可靠性与完备性，只有通过证明过的理论才是完美的，前面学过的很多正确的命题都可以通过用证明的方法来说明它们的正确性.如“等边对等角”、“平行四边形的对边相等”等.
    4. 画∠ACE=∠A是否也可以证明: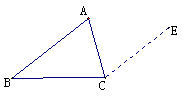
    ∠A+∠B+∠ACB=180°？
    　
    　
    　
    　
    　
    5. 你还有不同的证明方法吗？与同学交流.
    例如：过点A作EF∥BC.

    　

    思考：如图，∠α是△ABC的一个外角，∠α与△ABC的内角有怎样的大小关系？

    由三角形内角和定理，可以知道：

    ∠α=∠A+∠B,

    进而∠α＞∠A，

    ∠α＞∠B.

    三角形内角和定理的推论：

    1. 三角形的一个外角等于和它不相邻的两个内角的和；

    试题详情

    3.体会到添加辅助线可以帮助我们把不会解的新问题转化为会解的问题，是常用的数学方法.

    试题详情


    同步练习册答案