
针对本节课的知识点及能力要求,我编写了5道课后练习题.其中第1、2两题是基础训练题,巩固加深对“SAS”的理解.第3、4题主要是考察学生识图的能力,通过边角的加减来创造三角形全等的条件.第4题的变式练习能力要求较高,要求学生能够灵活运用所学知识综合运用.第5题仍是联系生活实际的一道题目,体现《课标》中“注重所学内容与现实生活的联系”.
探索三角形全等的条件(1)
班级 姓名 等第
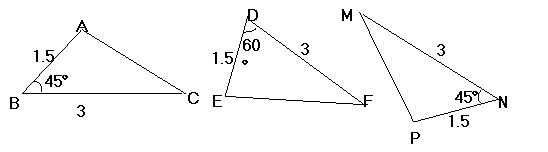
1、分别找出各题中的全等三角形,并说明理由.



|
(四)课堂小结,建立知识体系.
1、经历了剪纸、测量、画图等方法探索三角形全等条件的活动过程、积累数学活动经验.
2、归纳得出了两个三角形全等的条件--SAS,知到了有两边和其中一边的对角对应相等的两个三角形不一定全等,初步发展了推理能力.
附板书设计:
探索三角形全等的条件
探究活动一: 两个三角形全等至少要几个条件

 一个条件 行不通
两个条件 行不通 三个条件
一个条件 行不通
两个条件 行不通 三个条件
探究活动二: 全等三角形的识别方法:
 特殊------一般
特殊------一般
观察------猜想------验证------结论------应用
识别方法一:两边和它们的夹角对应相等的两个三角形全等.简写成“边角边”或“SAS”
例题讲解:例题 练习巩固
(三)例题教学,发挥示范功能
例题教学是课堂教学的一个重要环节,因此,如何充分地发挥好例题的教学功能是十分重要的.为此,我将充分利用好这道例题,培养学生有条理的说理能力,同时,通过对例题的变式与引伸培养学生发散思维能力.
首先,我将出示课本例1,并设计下列系列问题,让学生一步一步地走向“知识获得与应用”的理想彼岸.
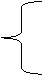
 例题1:例1:如图,AB=AD,
例题1:例1:如图,AB=AD,
∠BAC=∠DAC,请问:△ABC
和 △ADC是否全等?为什么?
问题1: 请说说本例已知了哪些条件,还差一个什么条件,怎么办?(让学生学会找图形中的隐含条件).
问题2: 你能用“因为……根据……所以……”的表达形式说说本题的说理过程吗?
问题3: △ADC可以看成是由△ABC经过怎样的图形变换得到的?
在探索完上述3个问题的基础上,对例题作如下的变式与引伸:
△ABC与△ADC全等了,你又能得到哪些结论?连接BD交AC于O,你能说明△BOC与△DOC全等吗?若全等,你又能得到哪些结论?
设计意图:这样设计的目的在于体现“数学教学不仅仅是数学知识的教学,更重要的发展学生数学思维的教学”这一思想.
在例题教学的基础上,为了及时的反馈教学效果,也为提高学生知识应用的水平,达到及时巩固的目的,我设计了如下两个练习:
1、基础知识应用
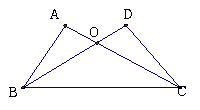
如图,在△ABC和△DCB中,BC是公共边,如果∠ABC=∠DCB,只要再有 = ,也能说明△ABC≌△DCB
2、讨论 :将“两边和它们的夹角对应相等”
改为“两边和其中一边的对角相等”这样的两个三角形还全等吗?
3、联系生活实际
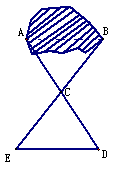 春节期间,几名学生在钵池山公园,测量一池塘两端A、B间的距离,设计了如下方案:如图,先在平地上取了一个可直接到达A、B的点C,再连接AC,BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测DE的长即为AB间的距离,你认为这种方案可行吗?并加以说明.
春节期间,几名学生在钵池山公园,测量一池塘两端A、B间的距离,设计了如下方案:如图,先在平地上取了一个可直接到达A、B的点C,再连接AC,BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测DE的长即为AB间的距离,你认为这种方案可行吗?并加以说明.
(一)创设情景,激发求知欲望
首先,我出示一个实际问题:
问题:开明中学为了提高学校硬件环境,到力达公司定做了一批三角形架用于教室摆放电视机,要求是所有的三角形必须全等.后勤部门为了使产品顺利过关,提出了明确的要求:要逐一检查三角形的三条边、三个角是不是都相等.部门职员小李提出了质疑:分别检查三条边、三个角这6个数据固然可以.但为了提高我们的效率,是不是可以找到一个更好的方法,只量一个数据可以吗?两个呢?……
然后,教师提出问题:小李已提出了这么一个设想,同学们是否可以和小李一起来攻克这个难题呢?
设计意图:这样设计的目的是既交代了本节课要研究和学习的主要问题,将数学问题与实际生活相结合,又能较好地激发学生求知与探索的欲望.同时让学生知道数学知识无处不在,应用数学无时不有.符合“数学教学应从生活经验出发”的新课程标准要求. (二)引导活动,揭示知识产生过程
数学教学的本质就是数学活动的教学,为此,本节课我设计了如下的系列活动,旨在让学生通过动手操作、合作探究来揭示“边角边”判定三角形全等这一知识的产生过程.
活动一:1、让学生通过画图或者举例说明,只量一个数据,即一条边或一个角不能判断两个三角形全等.
2、让学生就测量两个数据展开讨论.先让学生分析有几种情况:即边边、边角、角角.再由各小组自行探索.同样可以让学生举反例说明,也可以通过画图说明.
3、在两个条件不能判定的基础上,只能再添加一个条件.
活动二:讨论第一种情况:各小组每人用一张长方形纸剪一个直角三角形(只用直尺和剪刀),怎样才能使各小组内部剪下的直角三角形都全等呢?主要是让学生体验研究问题通常可以先从特殊情况考虑,再延伸到一般情况.
活动三:出示课本上的3幅图,让学生通过观察、进行猜想,再测量或剪下来验证.并说说全等的图形之间有什么共同点.
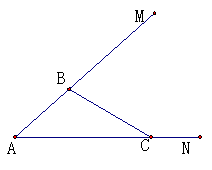

活动四:如图:(1)画∠MAN=50º;
(2)在AM、AN上分别截取AB=1.4cm,AC=2.3cm;
(3)连结BC,剪下所的△ABC,与同学所剪的三
角形比较,它们全等吗?
归纳总结:两边和它们的夹角对应相等的两个三角形全等.简写成“边角边”或“SAS”
设计意图:在探索三角形全等的条件这一重要内容上,设计了一系列的如:剪纸、画图、制作、猜想等各种形式的数学活动,创设了贴近学生生活的、有趣的问题情境,目的在于让学生“做数学”的特色,让学生在做中感受和体验,在做中主动获取数学知识,感悟三角形全等的数学本质,归纳和明晰三角形全等的条件,紧扣《课标》中“注重经历观察、操作、推理、想象等探索过程”的要求.
1、教学目标
在本课的教学中,不仅要让学生学会“边角边”这一全等三角形的识别方法,更主要地是要让学生掌握研究问题的方法,初步领悟分类讨论的数学思想.同时,还要让学生感受到数学来源于生活,又服务于生活的基本事实,从而激发学生学习数学的兴趣.为此,我确立如下教学目标:
知识目标:知道“边角边”这一三角形全等的识别方法.
能力目标:能利用“边角边”判别两个三角形全等,并解决一些简单的实际问题.
过程与方法:经历探索三角形全等条件的过程,体会分析问题的方法,积累数学活动的经验,
情感与态度:培养学生勇于探索、团结协作的精神.
2、剖析教材重难点
由于本节课是第一次探索三角形全等的条件,因此我确立了探究“边角边”这一识别方法作为教学的重点,而将其发现过程以及边边角的辨析作为教学的难点.所以,我采用让学生动手操作、合作探究、媒体演示等多种方式来突破难点.
3、教学具准备,教具:相关多媒体课件;学具:剪刀、纸片、直尺.画有相关图片的作业纸.
4、教法选择与学法指导
根据本节课的特点,我将采用“研究性学习”的教学方法,在课堂教学让学生动手“做数学”,让学生进行合作学习,在“做”的过程中体会分类讨论的数学思想方法,遵循“教是为了不教”的原则,让学生自寻方法、自觅规律、自得知识、自悟原理.
5、教学流程
2、在本章节之前,七年级学生已经通过《平面图形的认识(一)(二)》的学习,初步了解探索问题的一般方法与思路,已逐步形成了推理意识及有条理的表达意识.因此在教学中,不失时机的引导学生在各个活动自觉的思考,用自己的语言说明操作过程,并尝试解释其中的理由.
1、七年级学生的理解能力和思维特征和生理特征,学生好动性,注意力易分散,爱发表见解,希望得到老师的表扬等特点,所以在教学中应抓住学生这一生理心理特点,一方面要运用直观生动的形象,激发学生的兴趣,使他们的注意力始终集中在课堂上;另一方面要不断创造条件和机会,让学生发表见解,充分发挥学生学习的主动性,体现学生的主体地位.
2、课标要求
对于本节课内容课标要求:探索并掌握两个三角形全等的条件;注重所学内容与现实生活的联系,注重经历观察、操作、推理、想像等探索过程.初步建立空间观念,发展几何直觉;在探索并掌握两个三角形全等的条件,与他人合作交流的过程中,发展合情推理,进一步学习有条理的思考与表达.
1、 本节内容在教材中的地位与作用.
对于全等三角形的研究,实际是平面几何中研究封闭的两个图形关系的第一步.它是两三角形间最简单、最常见的关系.本节《探索三角形全等的条件》是学生在认识三角形的基础上,在了解全等图形和全等三角形之后进行学习的,它既是前面所学知识的延伸与拓展,又是后继学习探索相似形的条件的基础,并且是用以说明线段相等、角相等的重要依据.同时,《课标》将“边角边”这一识别方法作为五个基本事实之一,说明本节的内容对学生学习几何说理来说具有举足轻重的作用.因此,本节课的知识具有承上启下的作用.
2. 三角形的一个外角大于任何一个和它不相邻的内角。
三角形的一个外角大于任何一个和它不相邻的内角。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com