30.证明:作AF⊥直线CD,交CD的延长线于F,

∵AB⊥BC,CF⊥BC,∴四边形ABCF是矩形,

∵AB=BC,∴四边形ABCF是正方形,∴AB=AF=BC=CF,

∵∠ABE= ∠AFD=90°,在Rt△ABE和Rt△AFD中,AE=AD,AB=AF,

∴Rt△ABE≌Rt△AFD,∴BE=FD,

∵BC= CF,

∴BC-BE=CF-DF,即EC=CD.

29.有△ACF≌△BCD.

证明:∵△ABC为等腰直角三角形,∴∠ACB= 90°,AC=BC,

∵△CFD为等腰直角三角形,∴∠FCD=90°,CF=CD,

在△ACF和△BCD中, AC=BC,∠ACF=∠BCD,CF=CD,

∴△ACF≌△BCD.

28.证明:如答图所示,∵AB=DC,AE=DF,又∵CE=BF,∴CE+EF=FB+EF,即BE=CF,

∴△AEB≌△DFC,∴∠AEF=∠DFE,

在△AEF和△DFE中,AE=DF,∠AEF=∠DEF,EF=FE,

∴△AEF≌△DFE.∴AF=DE.

27.解:在AC上截取AB′=AB,在△ABD和△AB′D中,AB=AB′,∠1=∠2,AD=AD,

∴△ABD≌△AB′D,∴BD=B′D,∠B=∠3,

∵AB+BD=AC,AC=AB′+B′C,

　∴AB′+B′D=AB′+B′C,

∴B′D=B′C,∴∠4=∠C,

∵∠3=∠4+∠C,∴∠3=2∠C,

∴∠B= 2∠C,∴∠B:∠C=2:1

26.证明:∵AB=AC,∴∠ABC=∠ACB,

∵CE、BD是高,

∴∠CEB=∠BDC=90°,

在△CEB和△BDC中,∠EBC=∠DCB,∠CEB=∠BDC,BC=CB,

∴△CEB≌△BDC, ∴CE=BD.

23.②　 24.△ADB≌△AEC,△BOE≌△COD;△ADB≌△AEC,△BOE≌△COD, △AOE≌△AOD.　 25.ASA,SAS

17.AC=DF　 18.3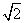;　 19.∠ACB=∠DBC　 20.∠D=∠B　 21.3　 22.AC=CA, ∠BAC= ∠DCA=90°. (2)∠BCA=∠DAC(ASA) (3)∠B=∠D(AAS) (4)BC=DA(HL)

30.如图所示,已知AB⊥BC,DC⊥BC,E在BC上,且AE=AD,AB=BC.

　　 求证:CE=CD.

A卷答案

29.如图所示,已知△ACB、△FCD都是等腰直角三角形,且C在AD上,AF 的延长线与BD交于E,请你在图中找出一对全等三角形,并写出证明它们全等的过程.

28.如图20所示,已知AB=DC,AE=DF,CE=FB,求证:AF=DE.