5、△AED≌△AFD;△AED≌△AFD,△BED ≌△CFD,△ABD≌△ACD.

　　 (1)答案:△ABD≌ACD,△ADE≌△ADF,△BDE≌△CDF,△AEM≌△AFM,△DEM ≌△DFM.

　　 (2)答案:△ABD≌△ACD,△ADE≌△ADF≌△BDE≌△CDF,△AEM≌△AFM ≌△DEM≌DFM.

4、已知:OM=ON,PM=PN.

　　 求证:OP平分∠AOB.

　　 证明:在△OPM和△OPN中,OM=ON,PM=PN,OP=OP,

∴△OPM≌△OPN,

∴∠POM=∠PON,故OP平分∠AOB.

3、A:已知:AB⊥BF,ED⊥BF,垂足分别为B,D,AE交BF于C,BC=DC.

　　 求证:DE=AB.

　　 证明:∵AB⊥BF,ED⊥BF,∴∠ABC=∠EDC=90°.

又∵∠BCA=∠DCE,BC=DE,

∴△BCA≌△DCE,∴AB=DE.

B: (1)可行,由(SAS)全等识别法,证△ACB≌△DCE.

　　 (2)可行;由(ASA)全等识别法,证△ABC≌△EDC.

　　 (3)得∠ABC=∠EDC;成立.

2、

A:解:∵AD⊥BC,∴∠ADB=∠ADC=90°,

在△ADB和△ADC中,∠ADB= ∠ADC=90°,∠DAB=∠DAC,AD=AD,

∴△ADB≌△ADC,∴BD=CD.

B:解:∵AC⊥AB,ED⊥DF,∴∠CAB=∠FDE=90°.

在Rt△ABC和Rt △DEF中,BC=EF,AC=DF,

∴Rt△ABC≌Rt△DEF,∴∠BCA=∠EFD,

∵AC⊥AB,∴∠ABC+ ∠BCA=90°,∴∠ABC+∠DFE=90°.

1、带③去.

解:③中已知两角及其夹边作三角形是成立的,即已知:∠A、∠B及AB,求作的△ABC是惟一的,因此,应带③去.

15.(2003,长沙)如图所示,若AC、BD、EF两两互相平分于点O, 请写出图中的一对全等三角形(只需写一对即可)_________.

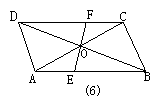
B卷答案

14.(2003,福州)如图所示,已知点A、B、C、D在同一条直线上,AB=CD,∠D= ∠ECA,EC=FD,求证:AE=BF.

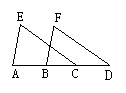
13.(2003,呼和浩特)如图5所示,在△ABC与△DEF中,如果AB=DE,BC=EF,只要再找出∠________=∠________或_________=_________,就可证明这两个三角形全等.

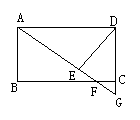
12.(2003,青岛)如图所示,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC.

根据上述条件,请在图中找出一对全等三角形,并证明你的结论.

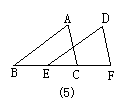
11.(2003,济南)如图4所示,△ABC中,已知AB=AC,要使AD=AE, 需要添加的一个条件是____________.