11．4　互逆命题

[教学目标]

8.小明用下面的方法画出了45°角：作两条互相垂直的直线MN、PQ，点A、B分别是MN、PQ上任意一点，作∠ABP的平分线BD，BD的反向延长线交∠OAB的平分线于点C，则∠C就是所求的45°角。你认为对吗？请给出证明。

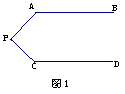
7.如图1，AB∥CD，

(1)∠A、∠P、∠C三角之间存在怎样的关系？用两种方法证明你的结论.

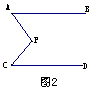
(2)如果将P点向右移，(如图2) AB∥CD，此时∠A、∠P、∠C三角之间存在怎样的关系？并证明你的结论.

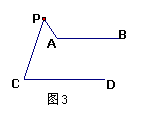(3) 如果将P点移到图3和图4的位置，此时∠A、∠P、∠C三角之间存在怎样的关系？并证明你的结论.

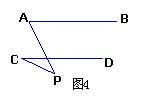
6.如图，△ABC中，　　　　　　 AB=AC，　

求证∠B=∠C.

5. 举反例说明下列命题是假命题.

(1)如果a+b＞0，那么a＞0，b＞0；

(2)面积相等的三角形是全等三角形.

(3)4条边相等的四边形是正方形.

(4)相等的角是对顶角.

(5)两直线被第三条直线所截,同位角相等.

(6)两边和其中一边的对角对应相等的两个三角形全等.

4.写出下列命题的逆命题，并判断原命题与逆命题的真假.

(1)如果|a|=|b|，那么a=b；　　

(2)如果a＞0，那么a²＞0；

(3)等角的补角相等；　　　　

(4)全等三角形的面积相等.

3.判断下列命题：

①等腰三角形是轴对称图形；

②若a>1且b>1，则a+b>2

③全等三角形对应角的平分线相等；④直角三角形的两锐角互余

其中逆命题正确的有(　　 )

A.1个　 B.2个　 C.3个　 D.0个

2.下列命题①同旁内角互补，两直线平行；②全等三角形的周长相等；③直角都相等；④等边对等角。它们的逆命题是真命题的个数是(　　 )

　A.1个　 B.2个　 C.3个　 D.4个

1.判断

(1)每一个命题都有逆命题(　　 )

(2)如果原命题是真命题，那么它的逆命题也一定是真命题(　　 )

(3)原命题是假命题，但它的逆命题可能是真命题(　　 )

4.原命题成立，它的逆命题一定成立吗？＿＿＿＿＿。请举一例：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

典型例题：

例1.指出下列命题中的互逆命题

(1)　　　 直角都相等

(2)　　　 同位角相等，两直线平行

(3)　　　 如果a+b>0, 那么a>0,b>0

(4)　　　 两直线平行，同位角相等

(5)　　　 相等的角都是直角

(6)　　　 如果a>0,b>0, 那么ab>0

例2.写出下列命题的逆命题，并指出其真假

(1)若ab=0,则a=0

(2)角平分线上的点到这个角的两边相等

(3)等腰三角形两底角相等

(4)四边相等的四边形是菱形

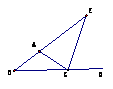
例3. 用符号“”写出下题的证明过程：已知：CE为△ABC外角∠ACD的平分线，CE交BA的延长线于E.求证：∠BAC＞∠B

能力训练：