
|
例1:写出下列命题的逆命题,并判断它是真命题还是假命题. (1)若ac2>bc2,则a>b; (2)角平分线上的点到这个角的两边距离相等; (3)若ab=0,则a=0. [分析]写出一个命题的逆命题,只需将命题的条件与结论交换一下则行.判断一个命题的真假,说它真,必须有根有据;而说它假,只要举一个反例,千万不能想当然. 解答 (1)逆命题为:若a>b,则ac2>bc2. 假命题,如c=0,ac2=bc2 (2)逆命题为:到角的两边距离相等的点在这个角的平分线上,真命题. (3)逆命题为:若a=0,则ab=0,真命题. 说明:1、真命题应是公理、定理、定义以及由它们推导出来的正确的结论,是无需证明大家一致公认的事实或一步一步推导出来的,而假命题只需举一个反例,即符合题设但不符合结论的例子. 2、这里仍要提供让学生多说的好机会,让学生多说才能多思,多说才能有条理地表述,让学生自己去举反例,让学生要有思考的过程,要注意这里不仅仅是命题的教学,更是几何的综合课堂. |
|
|
活动内容 |
师生互动思考与安排 |
|
情境一: 公元前6世纪,古希腊哲人泰勒斯利用影子测量了金字塔的高度,他自已还发现了三角形的一个特征:等腰三角形的两个底角相等,反过来说,要使三角形两角相等,它们的对边必须相等.这个发现我们现在看来很简单,可是在当时发现它们的确不易,其实这两个三角形的特征是两个定理,或者说是两个真命题. 问题: 1. 这两个命题有什么联系与区别? 2. 我们还学过类似的一些命题吗?如(平行线的判定与性质). 归纳:两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题. 说明:1. 这个情境,通过同学们熟悉的一组互逆命题引入,使学生能轻易总结出互逆命题的特征,归纳出它们的条件与结论的共性.再通过同学们之间的合作、交流、探索出类似的命题,从而能熟练掌握互逆命题的概念,会识别两个互逆命题. 2. 把一个命题的条件和结论互换就得到它的逆命题,所以每个命题都有逆命题. 交流: 1. 说出下列命题的逆命题,并与同学交流: (1)对顶角相等; (2)如果a2=b2,那么a=b; (3)直角三角形的两个锐角互余; (4)轴对称图形是等腰三角形; (5)正方形的4个角都是直角. 说明:1. (1)(3)(5)直接叙述它们的逆命题可能会有些困难,可以指导学生画出相关的图形分析命题的条件和结论. 问题: 1. 你能判断上述互逆命题的真假吗? (1)真,假;(2)假,真;(3)真,真;(4)假,真;(5)真,假. 说明:组织学生思考并交流各自判断命题真假的情况,以利于引导学生主动发现:一对互逆命题的真假性不一定相同. 问题2:说说你对一对互逆命题的真假性的看法,如果原命题是真命题,它的逆命题一定是真命题吗? 问题3:你是如何判断一个命题是假命题的. 例:如果a2=b2,那么a=b正确吗? (不正确,如:当a=2,b=2时,a2=b2,但a≠b,这样的例子称为反例). 说明:组织学生交流各自判断一个命题是假命题的方法,以利于引导学生体验并理解:说明一个命题是假命题只需举一个反例.这里既是学生学习互逆命题,同时也获得判断真假命题方法的好机会,也是对前面几何知识的回味,要让学生多思,举一反三. |
|
3. 能从“同位角相等,两直线平行”、“两直线平行,同位角相等”这两个基本事实出发,证明平行线的判定定理、平行线的性质定理,并能简单应用这些结论.
2. 回顾平行线判定定理的证明,引导学生不断感受几何演绎体系的思维方法,并通过新的思考和讨论,以利于学生主动参与本节课的教学活动.
1. 回顾平行线的判定和性质,能主动地区别这些互逆命题;
本节课通过创设 “等腰三角形等边对等角与等角对等边”的情境,让学生对比两者之间的联系与区别,从而得出互逆命题的概念.在此基础上,让学生举出平时遇到过的命题,并说出它的逆命题,且判定命题与它的逆命题的真假,使学生经历“探索--发现--猜想--证明”的过程,不断发展合乎逻辑的思考能力,最后通过具体例题巩固所学过的知识,并体会反面思考问题的方法,让学生懂得任何事物都是正反两方面的对立统一体.
4.小结
(1)图形的特殊的“位置关系”常常决定了有某种特殊的“数量关系”。比如,如果两直线平行(位置关系),那么内错角相等(数量关系).反过来,图形的特殊的“数量关系”常常决定了图形有特殊的“位置关系”.比如,如果内错角相等(数量关系),那么两直线平行(位置关系),从而体会形与数之间的内在联系;
(2)回顾我们曾探索得到的关于图形的“位置关系”和“数量关系”的互逆命题.
3.例题教学
本课时课本没有编排例题,建议在实际教学中另加一个计算题,为学生提供计算题书写的示范.比如,
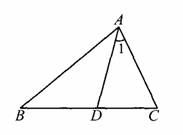
如图,点D在△ABC边BC上,且∠ADC=75°,∠1=∠B,求∠BAC的度数.
解:因为∠ADC=∠B+∠BAD(三角形的一个外角等于和它不相邻的两个内角的和),
∠1=∠B(已知),
所以∠ADC=∠1+∠BAD(等量代换),即∠ADC=∠BAC.
因为∠ADC=75°(已知),
所以∠BAC=75°(等量代换).
2.关于课本提供的探索活动
设计这个活动,实质是促使学生主动地把一个新问题转化为一个已经会解的问题,通过证明这个命题,又一次感受欧几里得“从基本事实出发,证明一个又一个命题”的方法,感受证明的必要性.
 教学中,可根据学生的实际情况,增加一个探索题.比如,从特殊到一般的探索或一题多解的探索。
教学中,可根据学生的实际情况,增加一个探索题.比如,从特殊到一般的探索或一题多解的探索。
1.关于课本提供的讨沦活动
这节课应进一步关注《标准》中“经历观察、实验、猜想、证明等数学活动,发展合情推理能力和初步的演绎推理能力,能有条理地、清晰地阐述自己的观点”等,这些过程性目标的落实。
课本提供了一个根据条件观察图形、做出猜想、证明猜想的讨论活动.设计这个活动,学生既经历合情推理,又经历演绎推理,不断发展初步的演绎推理能力.实际教学中,在学生做出猜想并表述各自的证明思路后,可以讨论以下问题:
(1)在图11-16中,如果DE//BF,∠B=∠D,那么你得到什么结论?证明你的结论.
(2)在图11-16中,如果AB//CD,DE//BF,那么你得到什么结论?证明你的结沦.
(3)小明从上面的讨论中,发观:“如果任意两个角的两条边分别互相平行,那么这两个角相等”.你认为小明的结论正确吗?为什么?
问题(1)、(2)构造了课本中讨论的关于图1l-16的一个命题的逆命题.设计这3个问题,实质是在不断依据有关平行线的互逆命题进行推理中,引导学生逐步认识探索图形的性质要关注图形的特殊的“位置关系”和“大小关系”的内在联系,体验数学活动充满着探索和创造,感受数学的严谨.对于问题(3),目的是引导学生关注反例的作用,小明所说的命题是假命题(符合命题条件的两个角可以互补),如果学生举反例有困难,教师可以提供适当帮助.但是,教学中无须进一步探索满足条件的两个角的大小关系,更不必给出“两条边互相平行的两个角相等或互补”的结沦,设计问题(3)仅仅是为了突出反例的作用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com