练习册

  • 练习册
  • 试题
     0  202460  202468  202474  202478  202484  202486  202490  202496  202498  202504  202510  202514  202516  202520  202526  202528  202534  202538  202540  202544  202546  202550  202552  202554  202555  202556  202558  202559  202560  202562  202564  202568  202570  202574  202576  202580  202586  202588  202594  202598  202600  202604  202610  202616  202618  202624  202628  202630  202636  202640  202646  202654  447090 

    2．如果一个三角形的三条高线恰好交于一个顶点，那么这个三角形是( ).

    　 A.锐角三角形　　 B.直角三角形　　 C.钝角三角形　　 D.等边三角形

    试题详情

    1．若三角形的三条边分别是8，10，a，则a的取值范围是( ).

    　 A.2 ≤ a ≤ 18　

    　 B.2 ≤ a ＜ 18

    　 C.2 ＜ a ≤ 18

    　 D.2 ＜ a ＜ 18

    试题详情

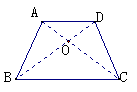    1.给下面的证明过程证明理由
    已知AB=DC，∠BAD=∠CDA
    求证：∠ABC=∠DCB
    证明：连结AC、BD交点为O
    在△ADB与△DAC中
    因为∠BAD=∠ADC(　　　　　　 )
    AD=DA(　　　　　　　　　　 )
    AB=DC(　　 　　　　　　　　)
    所以△ADB≌△DAC(　　　　　　　　　　 )
    所以BD=CA
    又在△ABC与△DCB中
    因为BD=CA(　　　　　　 )
    AB=DC(　　　　　　　 )
    BC=BC(　　　　　　　　 )
    所以△ABC≌△DCB(　　　　　　 )
    所以∠ABC=∠DCB
    2.证明：角平分线上的一点到这个角的两边距离相等.
    　
    　
    　
    　
    		 　

    试题详情

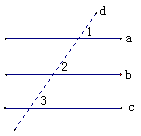    例1　 证明：如果两条直线都与第三条直线平行，那么这两条直线也互相平行.
    分析：已知：如图(2)直线a、b、c，
    b∥a，c∥a，求证：b∥c.
    证明：作直线a、b、c的截线d
    因为b∥a(已知)
    所以 ∠2=∠1(　　　　　　　　　 )
    因为c∥a (已知)
    所以∠3=∠1(　　　　　　　　　 )
    所以∠2=∠3(等量代换)
    所以b∥c(　　　　　　　　　　　　　　 )
    用符号“”简明表述上述的推理过程如下：
    b∥a∠2=∠1
    　　　　　　　 ∠2=∠3b∥c
    c∥a∠3=∠1
    你还有其他的方法证明b∥c吗？
    说明：这个例题可以让学生自己去探索，因为学生已有了这个结论，并且也有学生在解题时用过这个结论，如同三角形的内角和一样，此题的证明有多种方法，可让学生自己先说证明思路，教师切不可自己先讲，要让学生有自己的思考过程，也不可只讲一种访求了事，让学生体会多种方法.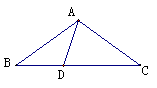
    例2　 如图，△ABC中，AB=AC，D在BC上，且BD=AD，DC=AC，求∠B的度数.
    分析：图中有三个等腰三角形，可用等边对等角的性质，再用方程的思想解题，列方程的依据是三角形内角和定理.
    解：∵AB=AC(已知)
    ∴∠B=∠C(等边对等角)
    同理，∠B=∠BAD，∠CAD=∠CDA.
    设∠B=x°，则∠C=x°，∠BAD=x°，
    ∴∠ADC=2x°, ∠CAD=2x°.
    在△ADC中，∵∠C+∠CAD+∠ADC=180°.
    ∴x°+2 x°+ 2x°=180 °.
    ∴x°=36 °.
    答：∠B的度数为36°.
    说明：这个几何计算题中没有知道任何一个角的度数，可是最后是让学生来求一个角的度数，同样也要让学生去体会，尝试用各种方法来解决，也要让学生有自己的思维过程，让学生体会数形结合，本例若想不到方程思想，或是找不到方程的依据，则问题就得不到顺利解放，究其原因，是对用代数方法解几何题较陌生，要加强训练加深印象.
    　
    　
    　
    　
    　
    　
    　
    　
    		 　

    试题详情

    活动内容
    		 师生互动思考与安排
    情境 ：
    如图1, AB∥CD，AB与DE相交于点G，
    ∠B=∠D.
    问题1：你由这些条件得到什么结论？
    如何证明这些结论？
    说明:充分发挥学生的主动性,去探索问题的结论.　　 图1
    在下列括号内填写推理的依据.　　　　　
    因为AB∥CD(已知)
    所以∠EGA=∠D(　　　　　　　　　　　　　 )
    又因为∠B=∠D(已知)
    所以∠EGA=∠B(　　　　　　 　　　　　　　　)
    所以DE∥BF(　　　　　　　　　　　　　　　 )
    上面的推理过程用符号“”怎样表达：
    分析:AB∥CD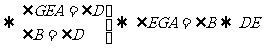∥BF
    问题2：还有不同的方法可以证明DE∥BF吗？
    问题3：在图(1)中，如果DE∥BF，∠B=∠D，那么你得到什么结论？证明你的结论.
    问题4：在图(1)中，如果AB∥CD，DE∥BF，那么你得到什么结论？证明你的结论.
    说明：1、问题3、4构造了课本中讨论的关于图(1)的一个命题的逆命题，实质是在不断依据有关平行线的的互逆命题进行推理中，引导学生逐步认识探索图形的性质要关注图形的“位置关系”和“大小关系”的内在联系，体验数学活动中充满着探索与创造，感受数学的严谨.
    2、课本提供的情景是让学生经历“观察--实验--猜想-证明”等活动，由合情推理到演绎推理，能有条理地、清晰地阐述自己的观点，从而不断发展初步的演绎推理的能力.
    3、实际中我们可以把图形演变为图2，再来让学生猜想，并能得出什么结论，并证明结论的正确性.从中让学生从中判断“如果任意角的两边分别互相平行，那么这两个角相等”这个命题正确与否.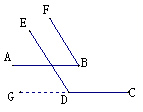
    　
    　
    　
    　
    　　　　　　　　　　　　　　　　　
    　　　　　　　　　　　　　　　　　　　 图2
    		 　

    试题详情

    3. 探索关于图形的“位置关系”和“数量关系”的互逆命题.

    试题详情

    2. 知道可以用不同的方式与方法证明同一个命题；

    试题详情

    1. 能使用合情推理和演绎推理证明一个命题；

    试题详情

    这节课创设了一个根据条件观察图形，做出猜想，证明猜想的活动情境，设计这个活动，使学生既经历合情推理，又经历演绎推理，不断发展初步演绎推理能力，从而使《标准》中“经历观察，实验猜想，证明”等数学活动，发展合情推理能力和初步的演绎推理能力，能有条理地、清晰地阐述自已的观点”这些过程性目标得到落实，再通过例题让学生知道可用不同的方式和方法证明同一个命题.

    试题详情

    1. 写出下列命题的逆命题，并判断原命题与逆命题的真假.
    (1)如果|a|=|b|，那么a=b；　　 (2)如果a＞0，那么a2＞0；
    (3)等角的补角相等；　　　　 (4)全等三角形的面积相等.
    2. 举反例说明下列命题是假命题.
    (1)如果a+b＞0，那么a＞0，b＞0；
    (2)面积相等的三角形是全等三角形.
    (3)4条边相等的四边形是正方形.
    (4)相等的角是对顶角.
    (5)两直线被第三条直线所截,同位角相等.
    (6)两边和其中一边的对角对应相等的两个三角形全等.
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    		 　

    试题详情


    同步练习册答案