
2.如图1所示,AB交CD于O点,OA=OB,再有OC=OD,就可用_________公理证明△AOC≌△BOD.
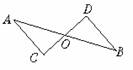
图1
1.只要三角形三边的长度确定了,这个三角形的_________就完全确定了.三角形的这个性质叫做三角形的_________.
5.有两边对应相等的两个三角形全等( )
4.四边形不具有稳定性( )
3.三角形具有稳定性( )
2.满足三个条件对应相等的两个三角形一定是全等三角形( )
1.两个三角形的三个角都分别是60°,30°,90°,则这两个三角形一定全等( )

利用三角形全等测距离
问题情境 想一想 练习

教学反思:通过一个实际的例子引出三角形全等的应用,生动、有趣、现实的例子会引起学生们的兴趣,引发他们去思考,并尝试用三角形全等的条件来解决实际问题。
|
想一想:
如图所示:A,B两点分别位于一个池塘的两端,小明和小颖想用绳子测量A,B两点间的距离。他们想出了这样的一个办法:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A,B两点间的距离。
小颖将条件标注在图中,并得出了结论:
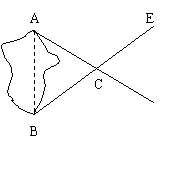
 因为有两边及其夹角对应相等,所以△ABC与△DEC全等, 这样AB就等于DE。
因为有两边及其夹角对应相等,所以△ABC与△DEC全等, 这样AB就等于DE。
你理解她的意思吗?
|
 CA=CD
CA=CD
|

|
∠ACB=∠DCE
你能说出每步的道理吗?
练习:P111 随堂练习 1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com