
2、黄河上某处的水位y与时间t之间有什么变化关系?
1、同学们每天从家里骑自行车上学,距离学校的路程s与时间t之间有什么变化关系?
12.(沪八)1平面上的点坐标练习一
第1题. 在坐标平面内点的位置与有序实数对 对应.
第2题. 如图所示的马所处的位置为(2,3).
⑴你能表示图中象的位置吗?
⑵写出马的下一步可以到达的位置.


第3题. 有序数对的意义是 ,利用有序数对,可以很准确地 .
第4题. 如果约定街在前,巷在后,则某单位在5街2巷的十字路口,用有序数对表示为( )
A.(2,5) B.(5,2) C.(5,5) D.(2,2)
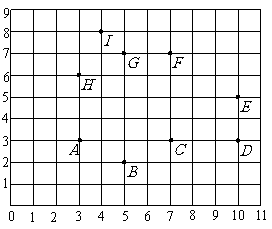
第5题. 如图,写出表示下列各点的有序数对:
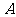 (_,_);
(_,_);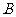 (5,2);
(5,2); (_,_);
(_,_); (_,_);
(_,_);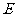 (_,_);
(_,_);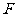 (_,_);
(_,_); (_,_);
(_,_); (_,_);
(_,_); (_,_);
(_,_);

第6题. 如图,表示下列图形格点的有序数对.
 (1,4)
(1,4) ( )
( ) ( )
( ) ( )
( )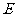 ( )
( )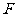 ( )
( )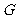 ( )
( )

第7题. 有序数对(2,3)和(3,2)相同吗?如果有序数对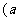 ,
, 表示某栋楼房中
表示某栋楼房中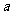 层楼
层楼 号房,那么有序数对(2,3)和(3,2)分别代表什么?
号房,那么有序数对(2,3)和(3,2)分别代表什么?
第8题. 如图,甲处表示三街与二巷的十字路口,乙处表示六街与六巷的十字路口,如果用(3,2)表示甲处位置,那么(3,2)→(3,3)→(3,4)→(3,5)→(3,6)→(4,6)→(5,6)→(6,6)表示从甲处到乙处的一条路线,请你用有序数对写出其他几种从甲处到乙处的路线.


第9题. 为了用一对实数表示平面内的点,在平面内画两条互相垂直的数轴,组成了 ,水平的数轴叫做 ,取 为正方向,铅直的数轴叫做 ,取 为正方向.
第10题. 画平面直角坐标系,标出下列各点:
点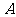 在
在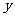 轴上,位于原点上方,距离原点2个单位长度;
轴上,位于原点上方,距离原点2个单位长度;
点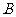 在
在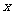 轴上,位于原点右侧,距离原点1个单位长度;
轴上,位于原点右侧,距离原点1个单位长度;
点 在
在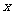 轴上方,
轴上方,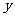 轴右侧,距离每条坐标轴都是2个单位长度;
轴右侧,距离每条坐标轴都是2个单位长度;
点 在
在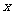 轴上,位于原点右侧,距离原点3个单位长度;
轴上,位于原点右侧,距离原点3个单位长度;
点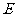 在
在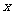 轴上方,
轴上方,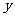 轴右侧,距离
轴右侧,距离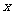 轴2个单位长度,距离
轴2个单位长度,距离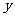 轴4个单位长度,依次连接这些点,你能得到什么图形?
轴4个单位长度,依次连接这些点,你能得到什么图形?
第11题. 如图,正方形 的边长为2,建立适当的平面直角坐标系,分别表示
的边长为2,建立适当的平面直角坐标系,分别表示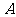 ,
,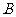 ,
, ,
, 四个点的坐标.
四个点的坐标.


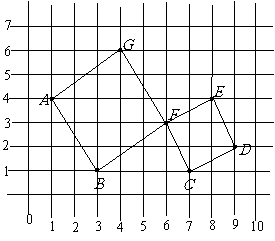
第12题. 如图是画在方格纸上的某一小岛的示意图.
⑴分别写出地点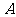 ,
, ,
,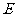 ,
,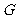 ,
,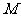 的坐标;
的坐标;
⑵(3,6),(7,9),(8,7),(3,3)所代表的地点分别是什么?


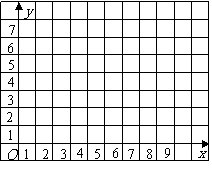
第13题. 在如图所示的坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.
⑴(1,2),(2,1),(6,1),(7,3);
⑵(3,3),(3,6),(5,2.5);
观察所得到的图形,你觉得它像什么?

第14题. 点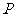 的坐标是
的坐标是 ,则
,则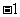 是点
是点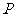 的 ,
的 , 是点
是点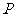 的 ,点
的 ,点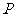 在第 象限.
在第 象限.
第15题. 已知点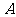 到
到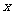 轴、
轴、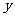 轴的距离分别为2和
轴的距离分别为2和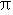 ,若
,若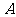 点的横坐标、纵坐标都是正值,则
点的横坐标、纵坐标都是正值,则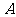 点坐标是 .
点坐标是 .
第16题. 点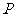 位于
位于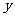 轴左方,距
轴左方,距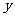 轴3个单位长,位于
轴3个单位长,位于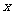 轴上方,距
轴上方,距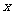 轴四个单位长,点
轴四个单位长,点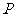 的坐标是 ( )
的坐标是 ( )
A.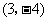 B.
B.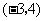 C.
C. D.
D.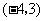
第17题. 在直角坐标系中,点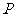
 ,
, 在第二象限,且
在第二象限,且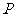 到
到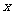 轴、
轴、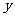 轴距离分别为3,7,则
轴距离分别为3,7,则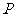 点坐标为( )
点坐标为( )
A. B.
B.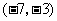 C.
C. D.
D.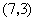
第18题. 已知点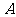 (1,2),
(1,2), 轴于
轴于 ,则点
,则点 坐标为 ( )
坐标为 ( )
A.(2,0) B.(1,0) C.(0,2) D.(0,1)
第19题. 已知点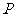
 ,
, 满足
满足 ,则点
,则点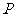 的位置是 ( )
的位置是 ( )
A.在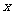 轴或
轴或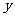 轴上
轴上
B.在第一、三象限坐标轴夹角平分线上
C.在第二、四象限坐标轴夹角平分线上
D.在坐标轴夹角平分线上
第20题. 正方形 中,
中,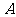 ,
,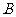 ,
, 坐标分别是
坐标分别是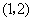 ,
,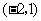 ,
, ,则顶点
,则顶点 坐标是 .
坐标是 .
第21题. 自画一个坐标系并描出下列各点:
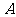 (2,1),
(2,1),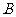 (-2,1),
(-2,1), (4,-3),
(4,-3), (4,3),
(4,3),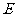 (-3,-2),
(-3,-2),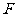 (3,2),
(3,2),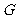 (0,-1),
(0,-1), (
(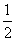 ,0).
,0).
根据在坐标系中描出的点观察: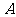 与
与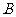 ,
, 与
与 ,
,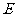 与
与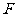 在位置上有何特点?并说明它们纵、横坐标各有什么特点.
在位置上有何特点?并说明它们纵、横坐标各有什么特点.
第22题. 如图,在所给的坐标系中描出下列各点的位置:
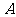
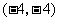 ,
,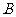
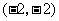 ,
,
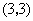 ,
,
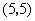 ,
,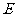
 ,
,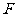
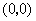 .
.
你发现这些点有什么关系?你能再找出一些类似的点吗?
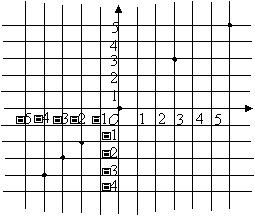

第23题. 在方格纸上建立一个平面直角坐标系,描出点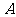
 ,
,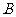
 ,连接
,连接 ,若点
,若点 为直线
为直线 上的任意一点,则点
上的任意一点,则点 的纵坐标是什么?
的纵坐标是什么?
⑴如果一些点在平行于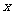 轴的直线上,那么这些点的纵坐标有什么特点?
轴的直线上,那么这些点的纵坐标有什么特点?
⑵如果一些点在平行于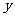 轴的直线上,那么这些点的横坐标有什么特点?
轴的直线上,那么这些点的横坐标有什么特点?

第24题. 在下图所示的直角坐标系中描出下列各点:
 ,
,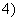 ;
; ,
,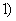 ;
; ,
,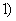 ;
; ,
, ;
;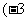 ,
, ;
; ,
,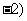 ;
;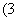 ,
, ;
;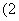 ,
, ;
; ,
,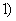 ;
; ,
,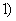 ;
; ,
,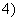 .
.
依次连结各点,观察得到的图形,你觉得它像什么?
第25题. 李强同学家在学校以东100m再往北150m处,张明同学家在学校以西200m再往南50m处,王玲同学家在学校以南150m处,如图,在坐标系中画出这三位同学家的位置,并用坐标表示出来.


第26题.  根据下图填表.
根据下图填表.
|
点 |
坐标 |
象限或坐标轴 |
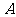 |
|
|
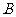 |
|
|
 |
|
|
 |
|
|
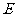 |
|
|
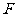 |
|
|
 |
|
|
本节课教学内容相对较多,有些知识难以理解,要分析透彻到位,通俗易懂。指导学生课后要加强复习巩固消化。教学过程中,知识点的应用让部分学生感到困难。数形结合思想让学生进一步地体会。
(六)布置作业
1、习题12.1 第 3、4题
2、补充:已知三点坐标A(4,3)、B(2,0)、C(-2,0),求以A、B、C为顶点的三角形ABC的面积?
(五)课堂小结(多媒体显示,学生自己归纳)
1、如何准确向他人描述某图形?
2、平面上点的坐标特点小结。
(四)随堂练习:
第9页的1、2题
(三)针对训练
1、点A(m-1,2m)在第二象限内,求m范围。若在x轴上呢?在第一、三象限坐标轴的夹角平分线上呢?
2、点A(m,m-1)与点B(3,2m)关于x轴对称,求m值,若关于y轴对称呢?
3、点(-3,4)到x轴、y轴距离各是多少?
(学生积极思考,参与活动,与同伴交流,上台演示)
④点到x轴距离是纵坐标的绝对值,点到y轴距离是横坐标绝对值。
(引导学生总结归纳,教师加以指导)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com