12．2等可能条件下的概率(一)(2)

3. 能借助概率的计算判断事件发生可能性的大小.

2. 进一步理解等可能事件的意义，会列出一些类型的随机实验的所有等可能结果(基本事件)，会把事件分解成等可能的结果(基本事件).

1. 在具体情境中进一步理解概率的意义，体会概率是描述不确定现象的数学模型.

本节课，我们从抛掷一枚均匀的骰子和摸球出发，在等可能条件下，让学生充分的探索和交流，一起感悟这个古典概型的两个基本特征，即试验结果的有限性和等可能性.能够在只通过一次试验中可能出现的结果的分析研究来求出随机事件的精确值.活动设计突出古典概型的基本特征(有限性、等可能性).

7．设计一种扑克牌游戏，使抽到红桃的概率是．

后花园

　　 智力操　 概率计算虽然简单，但是小冲经常出错．为了纠正他的错误，小明和小芳商量后决定针对他的问题，设计一些错题让他纠正．

　　 (1)口袋里有黄色和白色两种颜色的球，它们除颜色外都相同，任意取出1球，小冲认为得到黄球的概率是；

(2)小冲连续掷两枚硬币，列出的树状图如下：

　　 小冲由此得出两枚都是正面朝上的概率的．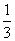

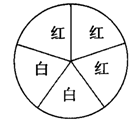
　　 (3)如图，转盘中的5个扇形完全相同，其中两个涂成白色，其余涂成红色．任意转动转盘，当转盘停止转动时，小冲认为指针指向红色部分的概率是．

　　 小冲看了题目，认为自己做得不错，小冲到底有没有错呢？请你当一次裁判．

6．连续掷两次骰子，利用树状图分别求满足下列条件的概率：

　　 (1)点数之和为5；(2)点数之和为1；(3)点数之和为偶数．

5．将分别标有数字1、2、3的3张卡片洗匀后，背面朝上放在桌面上．

　　 (1)随机地抽取1张，求抽到的卡片是奇数的概率；

　　 (2)随机地抽取1张作为十位上的数字(不放回)，再抽取1张作为个位上的数字，能组成哪些两位数？恰好是“32”的概率为多少？

拓展与延伸