
2、 写出下列几何体的体积表达式:
①长、宽、高分别为a、b、c的长方体的体积V=________;②棱长为a的正方体的体积V=______;③底面半径为r、高为h的圆柱的的体积V=_________;④底面半径为r、高为h的圆锥的体积V=_________;⑤半径为r的球的体积V=_____________。
1、
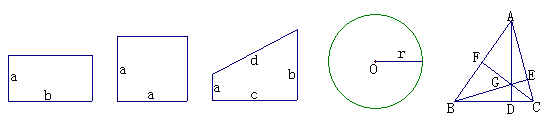 根据图形中的数据,计算图形的面积:
根据图形中的数据,计算图形的面积:
①长方形的面积S=_________;②正方形的面积S=_________;③直角梯形的面积S=_________________;④圆的面积S=__________;⑤若AD、BE、CF分别为△ABC的三条高,则△ABC的面积S=___________=____________=_____________。
3、 能据关系式求值,初步体会自变量和因变量之间的数值对应关系。
[自学指导]:
2、 能据情况,用关系式表示变量之间的关系。
1、 经历探索某些图形中变量之间关系的过程,体验一个变量的变化对另一个变量的影响。
5、点燃的蜡烛每分钟燃烧的长度一定。长为21㎝的蜡烛,点燃10分钟,变短3.6㎝。设点燃x分钟后,蜡烛还剩y㎝。
求:①y与x之间的关系式;②此蜡烛几分钟燃烧完?
4、在空中一个物体由静止到开始下落,它下落的距离与时间有下列关系:
|
时间t/秒 |
1 |
2 |
3 |
4 |
… |
n |
|
距离h/米 |
4.9×1 |
4.9×4 |
4.9×9 |
4.9×16 |
… |
? |
①在这个问题中,自变量是__________,因变量是__________;②当物体下落的时间为5秒时,它下落的距离是________米;③当物体下落的时间为n秒时,它下落的距离是__________米;④由此可知,物体由静止到开始下落,它下落的距离h(米)与时间t(秒)之间的关系式是_______________________。
3、 如图,长方形的宽为8,长为x,周长为y,面积为S:
如图,长方形的宽为8,长为x,周长为y,面积为S:
则①y与x之间的关系式为_________________;②S与x之间 的关系式为_____________;③当x=12时,y=______, S=_______;④当S=180时,x=_______,y=______;⑤当 x增加1时,y增加________,S增加________。
2、下表列出了弹簧长度与所挂物体的质量之间的关系。
|
弹簧长度/㎝ |
… |
12 |
15 |
16 |
18 |
20 |
|
挂物质量/㎏ |
… |
4 |
10 |
12 |
16 |
20 |
①在这个变化 过程中,自变量是_________,因变量是_________;②由数据可以看出,每加挂1㎏物体,弹簧会伸长________㎝,弹簧不挂物体时长度为________㎝;③弹簧长度y(㎝)与所挂物体的质量x(㎏)之间的关系式为______________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com