
3、合作探究
(1)整体感知
上节课我们学习了实数的相关概念,这节课我们将着重探讨实数的大小比较。
(2)四边互动
互动1:
师:有理数a的相反数是什么?非零的有理数a的倒数是什么?有理数a的绝对值是什么?请举手回答。
生:独立思考,举手回答,不断完善。
师:在实数范围内,上述结论是否正确呢?回答是肯定的。让学生回忆有理数范围内比较大小的方法,体会在实数范围内这些两个数大小的方法依旧成立。
互动2:
师:利用多媒体演示幻灯片3
例1
试估计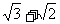 与π的大小关系.
与π的大小关系.
例2 请同学们使用计算器解答问题。
生:动手操作,交流解答结果。
师:在不使用计算器的情况下,你会比较3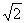 和2
和2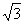 的大小吗?你想到哪些方法?
的大小吗?你想到哪些方法?
生:讨论交流后,举手上台板演
方法1:∵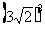 =18,
=18,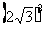 =12,∴3
=12,∴3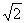 >2
>2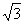
方法2:∵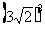 >4,
>4,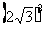 <4,∴3
<4,∴3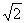 >2
>2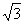
方法3:∵ =
=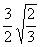 =
=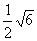 >1,∴3
>1,∴3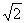 >2
>2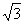
归纳可知:实数的大小比较,一般都可以通过使用计算器,用估算的办法达到目的,但有些实数的大小比较,还可以通过作差、作商等方法来达到目的。
2.课前热身
学生展示上节课的“实践活动”中剪纸拼图的结果,并进行相互评价。
1、 复习导入:
(1)无理数是怎样定义的?如何把实数进行分类?
(2) 实数与数轴上的点成怎样的对应关系?
在有理数范围内,加法,乘法具有哪些运算律?有理数的运算顺序是怎样的?
2、 会用估算的方法进行实数的大小比较
[教学过程]
1、 了解实数的相反数、倒数和绝对值的意义。
3.1415926<π<3.1415927.
也就是π≈3.1415926…,他是世界上第一个确定圆周率准确到7位小数的人.祖冲之又提出了用两个分数表示π的近似值.即22 7及355 113,分别称为π的约率和密度.
在祖冲之发现密率一千多年后,欧洲的安托尼兹(16世纪-17世纪)才重新发现了这个值
第2课时
[本课目标]
3.14,-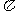 ,
,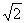 ,1.414,
,1.414,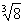 ,-
,-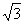 ,0,
,0,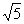 -1,0.1010010001…
-1,0.1010010001…
实数集合有:{ …}
有理数集合有:{ ...}
无理数集合有:{ …}
[板书设计]
|
课题:实数的概念 无理数的意义 实数的意义及分类 |
投影幕 |
[教学反馈]
我国古代数学家关于π的研究:
圆的周长与直径的比值是一个常数π,它是一个无理数,我们可以用有理数来近似表示它.
求无理数π的近似值,我国古代数学家早已作出了巨大的贡献,在东汉初年的数学书《周髀算经》里已经载有“周三径一”,称之为“古率”,就是说,直径是1的圆,它的周长是3.
到了西汉末年,刘歆(约分元前50年到公元23年)定圆周率为3.1547,到了东汉时代,张衡(公元78-139年)求得两个比,一是92 29=3.17241…,另一个是10,约等于3.1622.(印度数学家罗笈多也曾定圆周率为10,但已迟于张衡500多年.)
到了三国时,魏人刘徽(公元263年)创立了求圆周率的准确值的原理,他用割圆术求得圆周率的前三位数字是π≈3.14…,称为徽率.
到南北朝时代的祖冲之(公元429年-500年),他已推算出
6、实践探索
(1)
取若干个边长为1的正方形纸片,请用剪刀拼图的方法,作一个边长为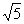 的正方形纸片。
的正方形纸片。
(2) 把下列各数填入相应的集合中:
5、学习小结
本课我们学习了实数的意义和分类,了解实数与数轴上的一一对应。
3、 达标反馈
判断正误:
① 无理数是无限小数
② 无限小数是无理数
③ 无理数是开方开不尽的数
④ 无理数不能用分数表示
⑤ 整数和分数统称实数
⑥ 数轴上的点表示实数
⑦ 有理数与数轴上的点成一一对应关系
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com