练习册

  • 练习册
  • 试题
     0  202497  202505  202511  202515  202521  202523  202527  202533  202535  202541  202547  202551  202553  202557  202563  202565  202571  202575  202577  202581  202583  202587  202589  202591  202592  202593  202595  202596  202597  202599  202601  202605  202607  202611  202613  202617  202623  202625  202631  202635  202637  202641  202647  202653  202655  202661  202665  202667  202673  202677  202683  202691  447090 

    3.一个正数的算术平方根是8，则这个数的相反数的立方根是(　　 )

    A.4　　 B.－4　　 C.　　 D.

    试题详情

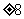
    2.一个数的立方根等于它本身，则这个数是(　　 )

    A.0　　 B.1　　 C.－1　 D.±1，0

    试题详情

    1.一个数的算术平方根与它的立方根的值相同，则这个数是(　　 )

    A.1　　 B.0或1　　 C.0　　 D.非负数

    试题详情

    3、若利用这个盒子和转盘做游戏，每次游戏时游戏者必须交游戏费1元，若游戏者所摸出的球上字母与转盘停止后指针对准的字母相同，则获得奖励2元，否则没有奖励，该游戏对游戏者有利吗？

    　
    　
    　
    　
    　
    　
    　

    试题详情

    2、如果不公平，该如何修改约定才能使游戏对双方公平？

    试题详情

    1、你认为这个游戏公平吗？为什么？

    试题详情

    3、盒中装有完全相同的球，分别标有“A”、“B”、“C”，从盒中随意摸出一球，并自由转动转盘(转盘被分成三个面积相等的扇形)，小刚和小明用它们做游戏，并设定如果所摸出的球上字母与转盘停止后指针对准的字母相同，则小明获得1分，如果不同，则小刚获得1分.

    试题详情

    1、如图所示的两个转盘中，当转盘停止转动时，指针若在每一个数上的机会相等，那么指针同时落在奇数上的概率是多少？
    　

    　

    2、两次连续转动如图所示的转盘

    ①求P(指针两次都指向红色区域)

    ②求P(指针两次都指向不同颜色区域)

    红
    　
    蓝
    　
    红
    　
    ③求P(指针两次指向相同颜色区域)　　　　　　　

    　

    (图2)

    试题详情

    例1：某商场为了吸引顾客，开展有奖销售活动，设立了一个可以自由转动的转盘，转盘等分为16份，其中红色1份、蓝色2份、黄色4份、白色9份，商场规定：顾客每购满1000元的商品，就可获得一次转动转盘的机会，转盘停止时，指针指向红、蓝、黄区域，顾客可分别获得1000元、200元、100元的礼品，某顾客购物1400元，他获得礼品的概率是多少？他分别获得1000元、200元、100元礼品的概率是多少？
    说明：
    1、首先让学生说出这位顾客有无获的一次转动转盘的机会？为什么？
    2、这个问题把几何概型转化为古典概型后在试验过程中共有多少个结果？获得礼品的结果有几次？怎样求获得礼品的概率？
    3、用同样的方法可求其余的概率.
    4、延伸：若某顾客购满2100元的商品，求获得礼品的概率是多少？两次同时获得1000元礼品的概率是多少？
    例2：在4m 远外向地毯扔沙包，地毯中每一块小正方形除颜色外完全相同，假定沙包击中每一块小正方形是等可能的，扔沙包1次，击中红色区域的概率多大？
    问题1：这个问题可转化为等可能条件下的概率(一)吗？
    问题2：在试验过程中，这些正方形除颜色外都相同，每扔一次沙包一次击中每一块小正方形的可能性都相同吗？
    问题3：在试验过程中每扔一次沙包所有可能发生的结果有多少个？击中红色区域的可能性结果有几个？概率是多少？
    延伸：若扔沙包2次，分别击中红、白的概率是多少？若扔沙包3次分别击中3种不同颜色区域的概率有多大？
    动手设计：
    设计一个转盘，使得指针指向红色区域的概率为1/2，指针指向黄色区域的概率为1/4，指针指向蓝色区域的概率为1/4.
    说明：以上例题研究的是由面积大小求概率，而本题正好相反，由概率到面积，引导学生通过探索得出结论：若指针指向某颜色区域的概率为n/m，那么该颜色区域面积占整个转盘面积的n/m.
    反馈练习：P课本207页练习1、2题.
    补充：如图中有四个可能转的转盘，每个转盘被分为若干等分，转动转盘，当转盘停止后，指针指向白色区域概率相同的是(　　 )
    A、转盘1与转盘3　　　 B、转盘2与转盘3
    C、转盘3与转盘4　　 　D、转盘1与转盘4

    　

    		 　

    试题详情

    活动内容
    		 师生互动思考与安排
    情境1：出示一个带指针的转盘，任意转动这个转盘，如果在某个时刻观察指针的位置.

    　

    问题1：这时所有可能结果有多少个？为什么？

    问题2：每次观察有几个结果？有无第二个结果？

    问题3：每个结果出现的机会是均等的吗？

    说明：根据学生的回答，适时揭示等可能条件下的概率(二)的两个特点：1、试验结果有无限个.2、每一个试验结果出现的等可能性.

    8
    　
    1
    　
    情境2：出示一个带指针的转盘，这个转盘被分成8个面积相等的扇形，并标上1、2、3……8，若每个扇形面积为单位1，转动转盘，转盘的指针的位置在不断的改变.

    　

    问题1：在转动的过程中当正好转了一周时指针指向每一个扇形区域机会均等吗？那么指针指向每一个扇形区域是等可能性吗？

    问题2：怎样求指针指向每一个扇形区域的概率？它们的概率分别是多少？

    问题3：在转动的过程中，当正好转了两周时呢？当正好转了n周呢？当无限周呢？

    说明：1、在问题1中让学生讨论得出求概率的方法：指针指向某个区域面积／整个转盘面积.让学生感知概率与指针经过的区域面积大小和整个转盘区域面积大小有关.但由于转盘区域面积一定.所以只与指针的指向区域面积有关，指针指向区域越大则概率越大.

    2、由本情境让学生自主探索，归纳出不论转多少周，指针指向每个不同号码的扇形区域的概率是相等的，且概率大小与转的周数无关，这样可把无限周问题转化为一周来解决，把无限事件转化为有限事件来处理，进而把这种类型的几何概型转化为古典概型的问题.

    情境3：(P205页，书图12-3)2个可以自由转动的转盘，每个转盘被分成8个相等的扇形，任意转动每个转盘.

    蓝
    　
    红
    　
    蓝
    　
    蓝
    　
    蓝
    　
    红
    　
    红
    　
    红
    　
    红
    　
    红
    　
    　　　　 　　　　　

    　

    问题1：本题可化为等可能性概率(一)的问题吗？

    问题2：第一个转盘转一周时，试验结果有几个，其中有几个结果指向红色区域？概率是多少？

    问题3：用同样的方法研究第二个转盘，则第二个转盘指向红色区域的概率是多少？

    问题4：哪一个转盘指向红色区域概率大？你认为概率大小与什么 因素有直接关系？

    问题5：根据正面求概率的方法若要改变这两个转盘指针指向红色区域的概率，需要改变什么？

    问题6：若把转盘变成正方形其余不变，结果是一样吗？若每个转盘中红色扇形的个数不变，但位置变化一下，结果还是一样吗？

    说明：1、通过问题4、5进一步使学生理解概率的大小是由事件发生的区域面积大小决定的.2、通过问题6的探索使学生理解几何概的概率大小与随机事件所在的区域形状、位置无关.

    师生共同小结：几何概率大小与___________、___________无关，只与___________有关.

    		 　

    试题详情


    同步练习册答案