
3. 不等式X-3>1的解集是( )
A.X>2 B. X>4
C.X-2> D. X>-4
2.下列说法正确的是( )
A.X=1是不等式-2X<1的解集
B.X=3是不等式-X<1的解集
C.X>-2是不等式-2X<1的解集
D.不等式-X<1的解集是X<-1
1.下列不等式的解集,不包括-4的是( )
A.X≤-4 B.X≥-4
C.X<-6 D.X>-6
㈠ 提出问题,引发讨论
1.
 不等式的性质
不等式的性质
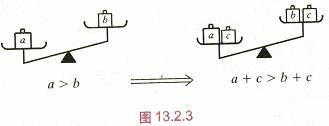
实验:如图在天平两边的称盘里一个倾斜的天平两边分别放有重物,其质量分别为a和b(a>b).
第一步:如果在两边的盘内分别加上等量的砝码c;
第二步: 如果在两边的盘内分别拿走等量的砝码c;
观察天平怎样变化?
性质1 不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变。
用式子表示为:如果a>b,那么,a+c>b+c, a-c>b-c。
想一想:如果天平两边的物体的质量同时扩大相同的倍数,天平还保持原状吗? (猜想)
练习:5>3 5×2__3×2 5×6__3×6 5×(-2)__3×(-2)
5×(-6)__3×(-6) 5×0__3×0
从中呢能发现什么?
性质2 不等式的两边都乘以(或除以)同一个正数不等号的方向不变。即如果a>b,并且c>0,那么ac>bc。
性质3 不等式的两边都乘以(或除以)同一个负正数不等号的方向改变。即如果a>b,并且c<0,那么ac<bc。
㈡ 导入知识,解释疑难
利用不等式的性质解不等式:
例1: 解不等式 ⑴x-7<8 ⑵3x<2x-3
解:⑴不等式的两边都加上7,不等号的方向不变,所以
x-7+7<8+7 即 x<15
⑵不等式的两边都减去2x,不等号的方向不变,所以
3x-2x<2x-3-2x 即 x<-3
例2:
解不等式 ⑴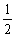 x>-3 ⑵-2x<6
x>-3 ⑵-2x<6
解:⑴不等式的两边都乘以2, 不等号的方向不变,所以
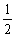 x×2>-3×2 即 x>-6
x×2>-3×2 即 x>-6
⑵不等式的两边都除以-2, 不等号的方向改变,所以
-2x÷(-2)>6÷(-2) 即 x>-3
作业 P60 1. 2. 3. 4.
前面我们学习了不等式的解集,明白了求不等式的解集的过程叫做解不等式,怎么解呢?不等式变形的规律是怎样的呢?为了解决这些疑问,我们必须要研究不等式的性质。
补充作业。
不等式的基本性质是什么?和方程的基本性质相比,有什么相同和不
同之处?本节课有什么收获?
4.已知x<2,能否推出3-2x>-1
培养学生逆向思维能力和从多个角度思考问题的能力
3.已知x>5,能否推出2x-3>7
2.已知ac2>bc2,能否推出a>b?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com