3．解下面的一元一次不等式组，并将解集表示在数轴上。

2．用两种方法解不等式－3≤(2x－1)／5＜6，并将不等式的解表示在数轴上。

　　 答案：解法一，直接化简不等式求解；解法二，变为不等式组求解。

　　 －1≤x＜3。

　　 问题探究与拓展活动

　　 通过本节课的学习，在教学过程中向学生渗透两种思想方法：类似方法，引导学生比较等式和不等式的联系，以探索新知识；数形结合的思想，用数轴表示解集。通过对这两种方法的阐述帮助学生提高探索新知识的能力。

　　 练习设计

　　 随堂练习设计

1．解不等式组，并用数轴表示不等式组的解。

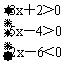
　　 答案：4／5＜x＜3

　　 (1)解出相关的不等式

　　 (2)画数轴找公共部分，从而解出不等式组

　　 本课总结

　　 在本节我们得到一元一次不等式组，以及一元一次不等式组的解集的概念。另外，还通过一元一次不等式的解，探讨了一元一次不等式组的解法，并进一步学习了解决简单的实际问题。本节教会学生怎样解一元一次不等式组，并引导他们发现一元一次不等式组的解集和一元一次不等式的解集的关系，通过具体实例让学生经历知识的拓展过程，同时重视不等式与不等式组的解集在数轴上的表示，让学生进一步感受数形结合的作用，逐步熟悉和掌握这一重要的思想方法。

　　 板书设计

§ 13.3　 一元一次不等式组

　　 一元一次不等式组的概念：将两个一元一次不等式结合在一起就得到了一个一元一次不等式组

　　 一元一次不等式组的解集：几个不等式的解集的公共部分叫做由他们组成的不等式组的解集

15．某旅游团有48人到某宾馆住宿，若全安排住宾馆的底层，每间住4人，房间不够；每间住5人，有一个房间没有住满5人，问该宾馆底层有客房多少间？

14．某工厂工人经过第一次改进工作方法，每人每天平均加工的零件比原来多

10个，因而每人在8天内加工了200个以上的零件，第二次又改进工作方法，每人每天平均又比第一次改进方法，改进方法后多做27个零件，这样只做了4天，所做的件数就超过前8天所做的数量。试问每个工人原来每天平均做几个零件？

13．解下列不等式组：

(1)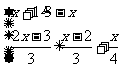　　　 (2)

12．如果不等式组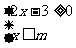无解，则m的取值范围是______。