
例1 解不等式组: 3x-1>2x+1 ①
2x>8 ②
让学生板演。
练习:解不等式组:
 3x-1>2x+1 ①
3x-1>2x+1 ①
2x<8 ②
5.概括总结。
(1)几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集。
(2)解一元一次不等式组的方法。
步骤:先求出不等式组中每一个不等式的解集,再求出它们的公共部分。找公共部分时,可以借助于数轴来帮助我们直观表示一元一次不等式组的解集。
4.练习。
让学生分别求出上面所列的不等式组中各个不等式的解集,并把各个解集在数轴上表示出来。
解:解不等式①得:x≥40
解不等式②得:x≤50。
那么,这个不等式组的解集是什么?
(让学生展开讨论,然后总结出不等式组的解集庄为两个不等式解集的公共部分。这个解集可以通过数轴直观地表示出来。)
让学生画数轴表示这两个不等式的解集的公共部分,找出不等式组的解集。
这两个不等式的解集在数轴上表示为:
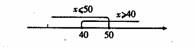
因此这个不等式组的解集为:40≤x≤50
即所提问题的答案为:大约需要40到50分钟才能将污水抽完。
3.不等式组的解集。
不等式组的解应使不等式组中各个不等式都成立。因此不等式组的解
集应是不等式组中各个不等式的解集的公共部分。
2.引人一元一次不等式组的概念。
由两个或两个以上的一元一次不等式合在一起,就得到了一个一元一次不等式组。注意:
(1)1200≤30x≤1500是不等式组的另一种形式。
(2)一元一次不等式组中的不等式可以有多个,但必须都是一元一次不等式。
1.分析。
因为每分钟抽水30吨,所以设需要。分钟才能将污水抽完,则x分钟抽的水是30x吨。
由题意可知,积存的污水在1200吨到1500吨之间,因此可列不等式组为:
1200≤30x≤1500
或
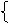 30x≥1200
30x≥1200
30x≤1500
(这个过程可以让学生自己来说,如果有的学生说不明白,可让其他学生补充,或者教师点拨、启发。)
让学生看课本中的问题3。
用每分钟可抽30吨水的抽水机来抽污水管道里积存的污水,估计积存 的污水在1200吨到1500吨之间,那么大约需要多少时间才能将污水抽完?
3.解下列不等式,并把解集在数轴上表示出来。
(1)3x-1> 2x+1;
(2)3-x≤1。
(为解不等式组做铺垫。)
1一什么叫方程的解?
2.解一元一次不等式的一般步骤是什么?
|
教师活动 |
学生活动 |
|
1.引导学生考虑课本第64页问题3。提示学生解决问题的关键是将问题用不等式表示。 2.肯定学生的答案,并提示学生观察不等式1200≤30x≤1500。 提问:此不等式的含义是什么?能否将此不等式化为多个不等式? 3.肯定学生的结论,并讲述一元一次不等式组的概念:将几个一元一次不等式合在一起就得到了一元一次不等式组,并鼓励学生举例说明。 4.引导学生分别完成对不等式 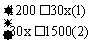 的解,提示学生不 的解,提示学生不等式组的解需要既满足不等式(1),又满足不等式(2),鼓励学生尝试说出不等式组。 5.肯定学生的答案并概括:不等式组的解集就是它所含不等式的解集的公共部分。 |
1.理解题意,找到不等量关系,并列出不等式1200≤30x≤1500。 2.积极思考,热烈讨论,说出不等式的含义为:30x≥1200并且30x≤1500,从而得出该不等式可拆成两个不等式的组合:1200≤30x;30x≤1500。 3.听取教师的总结,理解一元一次不等式的概念,并举例如: 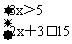 4.积极思考,认真计算,分别解出不等式(1)(2):x≥40;x≤50,将解集在同一数轴上表示,并在教师的提示下发现当x≥40并且x≤50时,两个不等式同时成立,从而说出不等式组的解。 5.听取老师的概括,类比方程组的解的定义,认识到不等式组的解集的概念。 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com