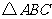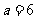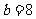3．中，，，则周长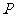的取值范围是______．

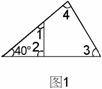
2．如图1，______．

1．两根木棒的长分别为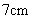和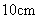．要选择第三根木棒，将它们钉成一个三角形框架，那么，第三根木棒长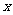()的范围是______．

教师准备：直尺、投影机．制作教具

学生准备：复习勾股定理，预习本节课内容．

教学过程

设计意图说明

一 复习引入 问题1：直角三角形有什么性质 ？ (1)有一个角是直角； (2)两个锐角互余 ； (3) 勾股定理：如果直角三角形两直角边分别为a，b，斜边为c，那么 ：a2 + b2 = c2 问题2：反之,一个三角形满足什么条件，才能是直角三角形呢? (有一个角是直角； 两个锐角互余) 问题3：猜想：让我们猜想一下，一个三角形各边长数量应满足怎样的关系式时，这个三角形才可能是直角三角形呢？这就是我们今天所要学习的内容 板书：14.1.2 直角三角形的判定 二 创设情境 古埃及人曾经用下面的方法画直角：将一根长绳打上等距离的13个结，然后用桩钉如图那样钉成一个三角形，他们认为其中一个角便是直角.你知道这是什么道理吗？(教具展示：用纸片钉好图形) 　　　　　　　　　 三 实验验证 探究新知： 1、 画图：试画出三边长度分别为如下数据的三角形,看看它们是一些什么形状的三角形: 　(1)a=3,b=4,c=5；(第一组同学画) 　(2)a=4,b=6,c=8; (第二组同学画) 　(3)a=6,b=8,c=10. (第3组同学画) (4)a=2,b=3,c=4　 (第4组同学画) 用展示台展示每一个组几个学生的图形,从而得出(在这三组数据中以(1)、(3)两组为边所画的三角形是直角三角形；以(2)、(4)两组为边所画的三角形不是直角三角形) 2、结合三角形三边长度的平方关系，你能猜一猜三角形的三边长度与三角形的形状有怎样的关系吗？ 而在这三组数据中,(1)、(3)两组都满足a2 + b2 = c2而(2)、(4))不满足. 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 3、归纳：(请一学生口述 师完善并板书) 勾股定理的逆定理： 如果三角形的三边长a、b、c满足　 a2 + b2 = c2 ， 　那么这个三角形是直角三角形。 几何语言： ∵a2 + b2 = c2　 ∴ΔABC为RtΔ 强调也可以是：满足较短的两边的平方和等于最长边的平方的三角形是直角三角形 三、知识应用 例1：设三角形三边长分别为下列各组数，试判断各三角形是否是直角三角形？ (1)7，24，25； (2)12，35，37； (3)13，11，9 教师板书过程： 解：(1)最大边为25 ∵72+242=625　 252 =625　 ∴72+242 =252 ∴以7, 24, 25为边长的三角形是直角三角形 第(2)题由学生板书，其余学生自己完成，教师观察学生完成情况。第(3)题请一生口述(特别指出要先找最大边)注意：①先找最大边②再判断三角形是否满足较短的两边的平方和等于最长边的平方(勾股定理的逆定理) 练习1：(用展示台完了一题再展示一题) 1、判断由线段a、b、c 组成的三角形是不是直角三角形？如果是，指出哪一条边所对的角是直角. (1)a=12,b=16,c=20　 (2) a=8,b=12,c=15 　(3) a=5,b=6,c=8　　　 (4) a:b:c=5:12:13 　 2、在△ABC中，三边长分别是8，15，17，则这个三角形是　　　 ，它的面积是　　　 . 　 3、△ABC中，若a=5，b=12，则当c=　　　 时，　　　　 ∠C=90 　 　 4、三角形的两边为3和5，要使它成为直角三角形，则第三边长为　　　　 . 　 例2、一个零件的形状如下图所示，按照规定这个零件中∠A 和∠DBC都是直角.量得各边尺寸如图所示，这零件符合要求吗？并说明理由。(请学生板书) 　　　　　　　　　　　　　　 　 练习2：变式训练(在原图擦去线段BD) 小明画了一个如图所示的四边形，其中AB=3，BC=12，CD=13，DA=4，∠A=90°，你能求出四边形ABCD的面积吗？(请一生口述) 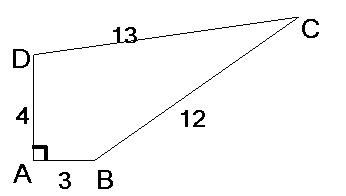练习3： 1、小蒋要求△ABC的的最长边上的高，测得AB=8cm，AC=6cm，BC=10cm。则可知最长边上的高_______ 2. 满足下列条件的△ABC,不是直角三角形的是(　　　 ) (A)a2 - b2 = c2　　　　　 (B)a:b:c=3:4:5 (C)∠C=∠A-∠B　　　 (D) ∠A:∠B : ∠C =3:4:5 3.在下列长度的各组线段中,能组成直角三角形的是(　　　 ) A. 5,6,7　 B. 32 ，42 ，52 　C. 5,11,12　　 D.　 5,12,13 四 活动竞赛 　每4位同学一组，首先请三位同学各说一个小于20的正整数，第4位同学判断由刚才所说的三个数为边是否会组成直角三角形；如果能组成直角三角形的请记录下来，看哪一个组最快而又准的把小于20的正整数为边又能构成直角三角形的数写完。(最后可得出常用的勾股数： 3，4，5　 6，8，10　 5，12，13　 8，15，17) 五 回顾反思：学生回顾本节的内容并归纳总结出： 1．勾股定理的逆定理：如果三角形的三条边长a、b、c有下列关系：a2+b2=c2．那么这个三角形是直角三角形．几何语言： ∵a2 + b2 = c2　 ∴ΔABC为RtΔ 　2．该逆定理给出判定一个三角形是否是直角三角形的判定方法．(注意要先找最大边) 3．利用勾股定理的逆定理判定一个三角形是不是直角三角形的过程主要是进行代数运算，通过学习加深对“数形结合”的理解． 六 探究：(如果有时间在课堂探究，没有时间就在课外探究) 给出一组式子： 32+42＝52，82+62＝102， 　 152+82＝172，242+102＝262．… 　(1)你能发现上面式子的规律吗?请你用发现的规律，给出第5个式子；(2)请你证明你所发现的规律． 七：课外作业：习题14.1：5，6.

由旧知识提出问题，设置悬念，引入课题，激发学习兴趣 　 　 　 　 　 由实际问题激发学生探究的欲望也体现出了数学来源于生活，设计教具的目的是为了让学生看起来更直观 　 　 　 通过实践，培养学生的动手能力，让学生体验数与形的内在联系 　 教师诱导，学生观察、分析并作结论，培养学生观察问题、分析问题和解决问题的能力 　 逐层深入，步步紧逼，引出勾股定理的逆定理 　 　 把知识的发现权交给学生，让他们在获取知识的同时，体验成功的喜悦 　 　 　 利用勾股定理的逆定理，识别一个三角形是否是直角三角形，突出本节课的重点 　 　 　 　 　 　 　 　 　 　 　 　 通过练习让学生熟练掌握用勾股定理的逆定理，识别一个三角形是否是直角三角形 　 　 　 　 　 　 这题既用了定理突出重点，又求面积为下面的变式训练作了铺垫 　 　 这题与第2题有所不同是求边可让学生有新鲜感 　 　 　 这题有二个答案可防止学生的思维定势，让学生考虑问题更全面 　 　 　 　 　 　 　 利用勾股定理的逆定理来解决实际问题既突出了重点又激发学生的兴趣 　 　 　 　 　 　 　 　 　 这个变式训练如果单独出现有一定的难度但在做完例2后就变得很容易了，突破了难点；又让学生有惊诧感觉，原来一个图形可有不同的题目，太有意思啦，学数学真好玩 　 　 　 　 　 　 　 　 　 　 这题要先用逆定理得出直角三角形求出面积再利用面积不变求出高 　 这题主要是从角和边来判断 　 　 　 这题我主要是设计B这个陷阱 　 　 设计竞赛可激发学生兴趣让学生在快乐中学习，同时也开放了课堂让学生真正做了课堂的主人 　 　 注意培养学生归纳总结的能力 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 这题有一定的难度，主要是想与中考接轨，锻炼学生的思维

　　 重点：理解和应用直角三角形的判定．

　　 难点：运用直角三角形判定方法进行解决问题．

　　 关键：运用合情推理的方法，对勾股定理进行逆向思维，形成一种判别方法．

知识与技能：掌握直角三角形的判定条件，并能进行简单应用．

　 过程与方法：通过“创设情境---实验验证----理论释意---实际应用---探究活动”的探索过程，让学生感受知识的乐趣

　 情感态度与价值观：激发学生解决的愿望，体会逆向思维所获得的结论．明确其应用范围和实际价值．

2、　　 为了加强公民的节水意识，某市制定了如下用水收费标准：每户每月的用水不超过10吨时，水价为每吨1.2元；超过10吨时，超过的部分按每吨1.8元收费，该市某户居民5月份用水x吨(x >10)，应交水费y元，请用方程的知识来求有关x和y的关系式，并判断其中一个变量是否为另一个变量的函数？

1、小明去商店为美术小组买宣纸和毛笔，宣纸每张3元，毛笔每支5元，商店正搞优惠活动，买一支毛笔赠一张宣纸．小明买了10支毛笔和x张宣纸，则小明用钱总数y(元)与宣纸数x之间的函数关系是什么？

　　 过程：

　　 根据题意可知：

　　 当小明所买宣纸数x小于等于10张时，所用钱数为：y=5×10=50(元)

　　 当小明所买宣纸数x大于10张时，所用钱数为：y=50+(x-10)×3=3x+20(元)

　　 结果：

　　 当0<x≤10时　 y=50

当x>10时　　 y=3x+20

2、《课堂感悟与探究》

　Ⅵ．活动与探究

1、习题14．1．1－1、2、3、4题．