
18.如图,某种旅行帽的帽沿接有两个塑料帽带,其中一个塑料帽带上有7个等距的小圆柱体扣,另一个帽带上扎有七个等距的扣眼,下表列出的是用第一扣分别去扣不同扣眼所测得帽圈直径的有关数据(单位:cm);
|
扣眼号数(x) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
帽圈直径(y) |
22.92 |
22.60 |
22.28 |
21.96 |
21.64 |
21.32 |
21.00 |
 (1)求帽圈直径y与扣眼号数x之间的函数关系式;
(1)求帽圈直径y与扣眼号数x之间的函数关系式;
(2)小强的头围约为68.94cm,他将第一扣扣到第4号
扣眼,你认为松紧合适吗?
17.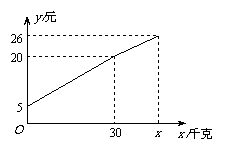 一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售;售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售;售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,
这时他手中的钱(含备用零钱)是26元,
问他一共带了多少千克土豆?
16.(1)已知点A(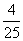 ,b)在函数
,b)在函数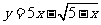 的图象上,求b的值.
的图象上,求b的值.
(2)已知点B(4,2)在函数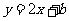 的图象上,试判断点C(
的图象上,试判断点C(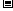 2,3)是否在此函数的图象上.
2,3)是否在此函数的图象上.
15.图①为深50cm的圆柱形容器,底部放一个长方形的铁块,现在以一定的速度往容器中注水,图②为容器上层到水面的距离随时间变化的图象,请回答下列问题:
 (1)求长方体的高度为多少厘米?
(1)求长方体的高度为多少厘米?
(2)求该容器注满水的时间为多少?
图① 图②
14.某巡逻船在码头外巡逻,离开码头的距离s(米)
与巡逻的时间t(分)的函数关系可用图中的曲
线表示.同时一艘游船到码头的距离s(米)与
时间t(分)的函数关系式为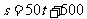 .
.
(1)在同一直角坐标系中画出函数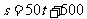
的图象;
(2)根据图象估计在哪些时刻游船和巡逻船到码
头的距离相同(时间精确到分,允许误差 分).
分).
13.点(1,m)、(2,n)在函数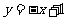 的图象上,则m、n间的等量关系是_________.
的图象上,则m、n间的等量关系是_________.
12.一游泳池长90m,甲、乙二人分别在游泳池的两边同
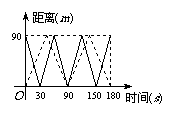 时朝另一边游泳.图中的实线和虚线分别为甲、乙与
时朝另一边游泳.图中的实线和虚线分别为甲、乙与
游泳池一边的距离随游泳时间的变化而变化的图象,
若不计转向时间,那么可以知道:
(1)甲游泳的平均速度是_____________;
(2)乙游泳的平均速度是_____________;
(3)从开始到3分钟时他们相遇的次数为____________. (第12题)
11.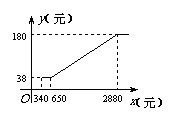 如图所示,某市自来水公司职工养老保险个人月缴费
如图所示,某市自来水公司职工养老保险个人月缴费
y(元)随个人工资x(元)的变化情况,则:
(1)小红的妈妈六月份工资为600元,该月她个人
应缴养老保险_________元;
(2)杨总工程师六月份工资为3000元,该月他个人
应缴养老保险_________元. (第11题)
10.已知,点P(4,b)在函数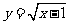 的图象上,则b
的图象上,则b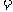 __________.
__________.
9.已知,点A的坐标是(2, ),AB
),AB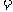 4,AB∥x轴,则点B的坐标是___________.
4,AB∥x轴,则点B的坐标是___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com