16.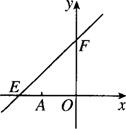如图，直线y=kx+6与x轴y轴分别交于点E，F.点E的坐标为(-8，0)，点A的坐标为(-6，0).

(1)求k的值；

(2)若点P(x，y)是第二象限内的直线上的一个动点，当点P运动过程中，试写出△OPA的面积S与x的函数关系式，并写出自变量x的取值范围；

(3)探究：当P运动到什么位置时，△OPA的面积为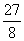，并说明理由.

(此题意在考查数形结合能力及坐标几何问题的综合应用.)

15.(12分)某服装厂现有A种布料70m，B种布料52m，现计划用这两种布料生产M、N两种型号的时装80套.已知做一套M型号的时装需要A种布料0.6m，B种布料O.9m，可获利45元，做一套N型号的时装需要A种布料1.1m，B种布料0.4m，可获利50元.若设生产N型号的时装套数为x，用这批布料生产这两种型号的时装所获的总利润为y元.

(1)求y与x的函数关系式，并求出自变量x的取值范围；

(2)该服装厂在生产这批时装中，当生产N型号的时装多少套时，所获利润最大?最大利润是多少?

(此题意在考查一次函数在解最大(小)值问题中的应用.)

14.(12分)网络时代的到来，很多家庭都接入了网络，电信局规定了拨号入网两种收费方式，用户可以任选其一：

A：计时制：O.05元/分；　 B：全月制：54元/月(限一部个人住宅电话入网).此外B种上网方式要加收通信费0.02元/分.

(1)某用户某月上网的时间为x小时，两种收费方式的费用分别为y₁(元)、y₂(元)，写出y₁、y₂与x之间的函数关系式.

(2)在上网时间相同的条件下，请你帮该用户选择哪种方式上网更省钱?

(此题意在考查一次函数与二元一次方程组.)

13.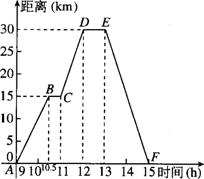(10分)小强骑自行车去郊游，右图表示他离家的距离.y(千米)与所用的时间t(小时)之间关系的函数图象，小明9点离开家，15点回家，

根据这个图象，请你回答下列问题：

(1)小强到离家最远的地方需几小时?此时离家多远?

(2)何时开始第一次休息?休息时间多长?

(3)小强何时距家21km?(写出计算过程)

(此题意在考查学生利用函数图象解决实际问题的能力及识图能力.)

12.(8分)画出函数y=2x+6的图象，利用图象：

(1)求方程2x+6=0的解；

(2)求不等式2x+6>0的解；

(3)若-1≤y≤3，求x的取值范围.

(此题意在考查一次函数与一元一次方程和一元一次不等式(组).)

11.(8分)已知一次函数图象经过(3,5)和(-4,-9)两点，

(1)求此一次函数解析式；(2)若点(a,2)在函数图象上，求a的值.

(此题意在考查待定系数法.)

10.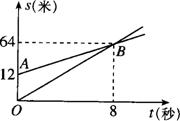如图：OB、AB分别表示甲、乙两名同学运动的一次函数　 图象，图中s和t分别表示运动路程和时间，已知、甲的速度比乙快，下列说法：①射线AB表示甲的路程与时间的函数关系；②甲的速度比乙快1.5米/秒；③甲让乙先跑了12米；④8秒钟后，甲超过了乙，其中正确的说法是(　　 )

(A)①②　　 (B)②③④　　 (C)②③　　 (D)①③④

(此题意在考查“数形结合”这一数学思想方法.)

9.“龟兔赛跑”讲述了这样的故事：领先的兔子看着缓慢爬行的乌龟，骄傲起来，睡了一觉，当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚，乌龟先到达了终点.用S₁，S₂分别表示乌龟和兔子所行的路程，t为时间，则下列图象中与故事相吻合的是(　　 )

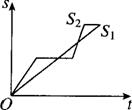
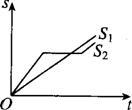
(A)　　　　　　　　　 (B)　　　　　　　　 (C)　　　　　　　 　　(D)

(此题意在考查学生的识图能力.)

8.右图是温度计的示意图，左边的刻度表示摄氏温度，右边的刻度表示华氏温度，华氏(°F)温度.y与摄氏温度(℃)x之间的函数关系式为(　　 )

(A)y=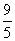x+32　 (B)y=x+40　　 (C)y=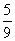+32　　 (D)y=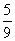x+31

(此题意在考查学生的观察、建模能力.)

7.若点A(2，4)在函数y=kx-2的图象上，则下列各点在此函数图象上的是(　　 )

(A)(0,-2)　　 (B) (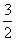,0)　　 (C) (8,20)　　 (D) (,)

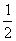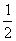(此题意在考查函数图象与其解析式的关系.)