多媒体放映干涸的水库的画面，让学生观看画面后简要描述画面所反映的现象，然后出示具体的问题情境：由于持续高温和连日无雨，某水库的蓄水量随着时间的增加而减少，干旱持续时间t(天)与蓄水量v(万米³)的关系如下图所示，回答下列问题：

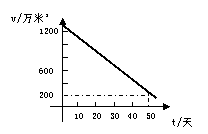
　　 (1)干旱持续10天，蓄水量为多少？连续干旱23天呢？

　　 (2)蓄水量小于400万米³时，将发生严重干旱警报，干旱多少天后将发生严重干旱警报？

　　 (3)按照这个规律，预计持续多少天水库将干涸？

　　 操作方法：先让学生独立思考，试试自己能否独立完成。然后老师进行分析，启发诱导，让学生学会识图，解决本节中的问题。

　　 分析：(1)这是一幅什么函数的图象？这个图象的每一点的横坐标和纵坐标分别表示什么？

　　 (2)要找到干旱持续10天后的蓄水量。先找到横轴上的10，然后过这点作x轴的垂线与直线有交点，然后相应地找到交点的纵坐标(边讲边演示，或者请学生边讲边演示)

　　 (3)回答第(2)问时方法与上相同。

　　 (4)水库干涸意味着水库里的蓄水量为多少？怎样找到蓄水量是0的这一点？

　　 本题反思：

1、通过对本题的探索，你在观察函数图象上有哪些收获？

5.解：设y=kx+b，则：0= -2k+b，b=2k………①

当x=0时，y=b；当y=0时，x= -。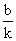

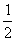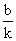S=︳b︳︱-︱=10…………………②

由①.②联立方程组，得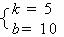：或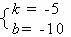

所以一次函数的解析式是：

y=5x+10或y= -5x-10

4.解：(1)由题意设：y-3=kx，则将x=2，y=7代入得7-3=2k，所以k=2.。故y与x的函数关系式是y=2x+3.(2)当x=0时，y=3；当y=0时，x= -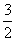。故它与坐标轴的交点坐标是(0，3).(-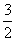，0)

3.解：设一次函数式为：y=kx+b，则有：

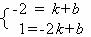　　 ，解得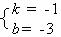：。所以一次函数式是：y=-x-3.

1.D　　　　　　　　　　　　 2. A

1.m<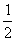且m≠-4　　　　　　　 2.<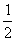， 一.三.四　　　　　　　 3.C　　　　　　　 4.D

第四课时

1.-3　　　　 2.±3　　　　 3.D　　　　 4.C　　　　 5.B　　　 6.略

第三课时

1.-2　　　　　 2.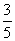　　　　　　 3.C　　　　　　　 4. B

第二课时

5.某一次函数的图象与坐标轴所围成的三角形的面积是10，且过点(-2，0)，求该一次函数的解析式.

第一课时

4.已知y-3与x成正比例，且x=2时，y=7，求：(1)y与x的函数关系式.(2)其图象与坐标轴的交点坐标.