
2.能用待定系数法求一次函数,用一次函数表达式解决有关现实问题.
1.理解待定系数法;
体会解决问题方法多样性,发展创新实践能力。
教学重点
灵活运用知识解决相关问题.
教学难点
灵活运用有关知识解决相关问题.
教学方法
实践─应用─创新.
教具准备
多媒体演示.
教学过程
1.提出问题,创设情境
我们前面学习了有关一次函数的一些知识及如何确定解析式,如何利用一次函数知识解决相关实践问题呢?
这将是我们这节课要解决的主要问题.
Ⅱ.导入新课
下面我们来学习一次函数的应用.
例1 小芳以200米/分的速度起跑后,先匀加速跑5分钟,每分提高速度20米/分,又匀速跑10分钟.试写出这段时间里她跑步速度y(米/分)随跑步时间x(分)变化的函数关系式,并画出图象.
分析:本题y随x变化的规律分成两段:前5分钟与后10分钟.写y随x变化函数关系式时要分成两部分.画图象时也要分成两段来画,且要注意各自变量的取值范围.
解:y=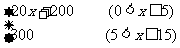
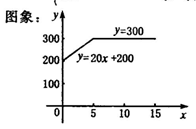
我们把这种函数叫做分段函数.在解决分析函数问题时,要特别注意自变量取值范围的划分,既要科学合理,又要符合实际.
例2 A城有肥料200吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡.从A城往C、D两乡运肥料费用分别为每吨20元和25元;从B城往C、D两乡运肥料费用分别为每吨15元和24元.现C乡需要肥料240吨,D乡需要肥料260吨.怎样调运总运费最少?
通过这一活动让学生逐步学会应用有关知识寻求出解决实际问题的方法,提高灵活运用能力.
教师活动:
引导学生讨论分析思考.从影响总运费的变量有哪些入手,进而寻找变量个数及变量间关系,探究出总运费与变量间的函数关系,从而利用函数知识解决问题.
学生活动:
在教师指导下,经历思考、讨论、分析,找出影响总运费的变量,并认清它们之间的关系,确定函数关系,最终解决实际问题.
活动过程及结论:
通过分析思考,可以发现:A──C,A──D,B──C,B──D运肥料共涉及4个变量.它们都是影响总运费的变量.然而它们之间又有一定的必然联系,只要确定其中一个量,其余三个量也就随之确定.这样我们就可以设其中一个变量为x,把其他变量用含x的代数式表示出来:
若设A──Cx吨,则:
由于A城有肥料200吨:A─D,200─x吨.
由于C乡需要240吨:B─C,240─x吨.
由于D乡需要260吨:B─D,260─200+x吨.
那么,各运输费用为:
A──C 20x
A──D 25(200-x)
B──C 15(240-x)
B──D 24(60+x)
若总运输费用为y的话,y与x关系为:
y=20x+25(200-x)+15(240-x)+24(60+x).
化简得:
y=40x+10040 (0≤x≤200).
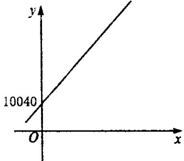
由解析式或图象都可看出,当x=0时,y值最小,为10040.
因此,从A城运往C乡0吨,运往D乡200吨;从B城运往C乡240吨,运往D乡60吨.此时总运费最少,为10040元.
若A城有肥料300吨,B城200吨,其他条件不变,又该怎样调运呢?
解题方法与思路不变,只是过程有所不同:
A──C x吨 A──D 300-x吨
B──C 240-x吨 B──D x-40吨
反映总运费y与x的函数关系式为:
y=20x+25(300-x)+15(240-x)+24(x-40).
化简:y=4x+10140 (40≤x≤300).
由解析式可知:
当x=40时 y值最小为:y=4×40+10140=10300
因此从A城运往C乡40吨,运往D乡260吨;从B城运往C乡200吨,运往D乡0吨.此时总运费最小值为10300吨.
如何确定自变量x的取值范围是40≤x≤300的呢?
由于B城运往D乡代数式为x-40吨,实际运费中不可能是负数,而且A城中只有300吨肥料,也不可能超过300吨,所以x取值应在40吨到300吨之间.
总结:
解决含有多个变量的问题时,可以分析这些变量间的关系,选取其中某个变量作为自变量,然后根据问题条件寻求可以反映实际问题的函数.这样就可以利用函数知识来解决了.
在解决实际问题过程中,要注意根据实际情况确定自变量取值范围.就像刚才那个变形题一样,如果自变量取值范围弄错了,很容易出现失误,得到错误的结论.
Ⅲ练习
从A、B两水库向甲、乙两地调水,其中甲地需水15万吨,乙地需水13万吨,A、B两水库各可调出水14万吨.从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米.设计一个调运方案使水的调运量(万吨·千米)最少.
解答:设总调运量为y万吨·千米,A水库调往甲地水x万吨,则调往乙地(14-x)万吨,B水库调往甲地水(15-x)万吨,调往乙地水(x-1)万吨.
由调运量与各距离的关系,可知反映y与x之间的函数为:
y=50x+30(14-x)+60(15-x)+45(x-1).
化简得:y=5x+1275 (1≤x≤14).
由解析式可知:当x=1时,y值最小,为y=5×1+1275=1280.
因此从A水库调往甲地1万吨水,调往乙地13万吨水;从B水库调往甲地14万吨水,调往乙地0万吨水.此时调运量最小,调运量为1280万吨·千米.
Ⅳ.小结
本节课我们学习并掌握了分段函数在实际问题中的应用,特别是学习了解决多个变量的函数问题,为我们以后解决实际问题开辟了一条坦途,使我们进一步认识到学习函数的重要性和必要性.
Ⅴ.课后作业
习题11.2─7、9、11、12题.
利用一次函数知识解决相关实际问题.
|
问题与情境 |
师生活动 |
设计意图 |
|
活动1 复习引入 1、 直线y=2x-3与X轴交点坐标为 ,与y轴交点坐标为 . 2、若直线y=kx+b(k≠0)与直线y=-3x平行,且与y轴交点的纵坐标为2,则k= ,b= . 3、若一次函数y=kx+b(k≠0),当自变量x=3时函数值y=5,当自变量x=-4时函数值y=-9,你能求出这个一次函数的解析式吗?你是如何求的? 活动2 例1:已知一次函数的图象过点(2,3)与(-1,-3),求这个一次函数的解析式。 |
教师出示问题1、2 学生思考、完成问题, 并举手发言,讲明解题思路和依据. 针对学生的回答,教师适当补充 教师出示问题3 学生思考并回答 教师引导学生分析强调: 求一次函数解析式的关键是求出k、b的值. 教师引导学生分析:可以设为解析式的一般形式y=kx+b,这样就转化为引入的问题3类型 教师板书解题过程. |
复习一次函数和坐标轴的交点,以及一次函数与正比例函数的图象和解析式的关系,本节内容铺垫. 让学生初步了解待定系数法,以及用待定系数法求一次函数的解析式的过程. |
|
我们解决例1的方法就是待定系数法 1、什么是待定系数法呢? 2、你能说出用待定系数法确定函数解析式的步骤吗? 练习1: (1)已知一次函数的图象经过点(-2,5)和点(1,1),求这个一次函数的解析式 (2)已知一次函数经过点(0,3)和点(2,1),求这个一次函数的解析式. 活动3 例2:已知一次函数的图象如图:  (1)求此函数的解析式; (2)求该直线和坐标轴围成的三角形的面积. 练习2: 已知一次函数的图象如下图所示,求函数的解析式及其图象与坐标轴围成的三角形的面积. 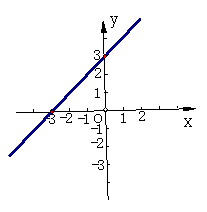 活动4 例3: 已知一次函数的图象经过点A(-2,6),且平行于直线y=-x (1)求这个函数的解析式; (2)求该一次函数的图象与坐标轴围成的三角形的面积。 活动5 小结、布置作业 小结: 通过本节课的学习,你有哪些收获? 1、确定一次函数的解析式需要 个条件;关键是 . 2、用待定系数法求函数解析式的一般步骤是什么? 布置作业: 反馈练习: 1、已知一次函数图象经过点(0,-3)和点(2,1),求其解析式. 2、已知一次函数的图象经过点(-1,3),且平行于直线y=2x,求其解析式. |
教师介绍带定系数法: 待定系数法是通过先设出函数的解析式,再根据条件列出方程或方程组求出解析式中未知的系数,从而得出函数解析式的方法. 师生共同总结: (1)设关系式; (2)代入对应值; (3)解方程(组); (4)代入关系式,得出函数解析式. 找一名学生板演问题2,其他学生独立完成练习 教师巡视,个别指导. 观察问题2,(0,3)实际是直线与y轴的交点,可直接得出:b=3,于是可设解析式为y=kx+3,进而求解. 师问:你能从图中读出什么信息? 学生观察图形,并回答问题. 分析:通过读图所得,可把该题转化为练习1中(2)的类型,从而进行求解. 学生完成解题过程 找个别同学演示 教师要关注学生是否能用不同的方法求解. 学生独立完成练习,教师巡视,并个别指导. 学生思考问题,举手发表自己的看法,教师可以适当引导. 师生分析:由平行于直线y=-x可知一次函数中的k=-1. 由学生独立完成解题过程. 学生举手发言,教师可适当给出提示: 1、确定一次函数的解析式需要 个条件;关键是 . 2、用待定系数法求函数解析式的一般步骤是什么? 作业:目标P8 课本P35 :5 学生在测验本上完成教师巡视 |
使学生明确什么是待定系数法,会说出用待定系数法确定函数解析式的步骤. 巩固待定系数法,让学生了解只需要两个条件就能确定出一次函数的解析式。 让学生学会观察图形, 使学生进一步掌握用待定系数法求一次函数的解析式,同时复习巩固在坐标系中如何求面积. 培养学生独立的观察能力及分析问题解决问题的能力。 把求一次函数的解析式同一次函数的性质相联系,培养学生综合分析问题的能力. 使学生掌握,如何离开具体的函数图象,求函数图象与两坐标轴围成的三角形的面积。 检测学生掌握的情况 |
|
|
板 书 设 计 |
11.2.2 一次函数(3) --用待定系数法求一次函数的解析式 例1、解:设函数解析式为: 用待定系数法求函数解析式的步骤:   Y=kx+b(k≠0),则: 1、 Y=kx+b(k≠0),则: 1、2k+b=3 k=2 2、 -k+b=-3 解得: b=-1 3、 所以,函数解析式为y=2x-1 |
||
|
课 后 反 思 |
|
||
2、难点:结合一次函数的性质,用待定系数法确定一次函数的解析式.
1、重点:用待定系数法求一次函数的解析式;
4、通过引入待定系数法的过程,向学生渗透转化的思想,培养学生分析问题,解决问题的能力.
3、能根据函数图象确定一次函数的表达式,并由此进一步体会数形结合的思想;
2、能结合一次函数的图象和性质,灵活运用待定系数法求一次函数解析式;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com