2.在画实际问题中的一次函数图象时，要考虑自变量的取值范围，画出的图象往往不再是一条直线.

1.一次函数y＝kx+b,当x＝0时，y＝b；当y＝0时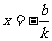，.所以直线y＝kx+b与y轴的交点坐标是(0,b),与x轴的交点坐标是；

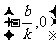5.陈华暑假去某地旅游，导游要大家上山时多带一件衣服，并介绍当地山区海拔每增加100米，气温下降0.6℃．陈华在山脚下看了一下随带的温度计，气温为34℃，乘缆车到山顶发现温度为32.2℃．求山高．

4.一次函数y＝kx+b(k≠0)的图象经过点(3,3)和(1,-1)．求它的函数关系式，并画出图象．

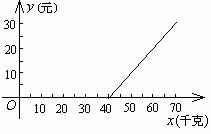
3.如图是某长途汽车站旅客携带行李费用示意图．试说明收费方法，并写出行李费y(元)与行李重量x(千克)之间的函数关系．

2.写出两个一次函数，使它们的图象都经过点(-2,3)．

1.根据下列条件写出相应的函数关系式．

(1)直线y＝kx+5经过点(-2,-1)；

(2)一次函数中，当x＝1时，y＝3；当x＝-1时，y＝7．

2．虽然题意并没有要求写出函数的关系式，但因为要求x＝5时，函数y的值，仍需从求函数解析式着手．

解 由题意，得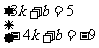

解这个方程组，得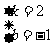

这个函数解析式为y＝2x-1

当x＝5时，y＝2×5-1＝9．

例2 已知一次函数的图象如下图，写出它的关系式．

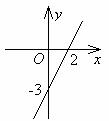
分析 从“形” 看，图象经过x轴上横坐标为2的点，y轴上纵坐标是-3的点．从“数”看，坐标(2,0),(0,-3)满足解析式．

解 设：所求的一次函数的解析式为y＝kx+b(k≠0)．

直线经过点(2,0),(0,-3),把这两点坐标代入解析式,得

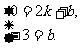　 解得　

所以所求的一次函数的关系式是．

例3 若直线y＝-kx+b与直线y＝-x平行，且与y轴交点的纵坐标为-2；求直线的表达式.

分析 直线y＝-kx+b与直线y＝-x平行，可求出k的值,与y轴交点的纵坐标为-2,可求出b的值.

解 因为直线y＝-kx+b与直线y＝-x平行，所以k＝-1,又因为直线与y轴交点的纵坐标为-2,所以b＝-2,因此所求的直线的表达式为y＝-x-2.

Ⅳ．课时小结

本节课，我们讨论了一次函数解析式的求法。求一次函数的解析式往往用待定系数法，即根据题目中给出的两个条件确定一次函数解析式y＝kx+b(k≠0)中两个待定系数k和b的值；

Ⅴ．课后作业

2．这个问题是与实际问题有关的函数，自变量往往有一定的范围．

问题3 若一次函数y＝mx-(m-2)过点(0,3)，求m的值．

分析 考虑到直线y＝mx-(m-2)过点(0,3)，说明点(0,3)在直线上，这里虽然已知条件中没有直接给出x和y的对应值，但由于图象上每一点的坐标(x,y)代表了函数的一对对应值，它的横坐标x表示自变量的某一个值，纵坐标y表示与它对应的函数值．所以此题转化为已知x＝0时，y＝3，求m．即求关于m的一元一次方程．

解 当x＝0时，y＝3．即：3＝-(m-2)．解得m＝-1．

这种先设待求函数关系式(其中含有未知的常数系数)，再根据条件列出方程或方程组，求出未知系数，从而得到所求结果的方法，叫做待定系数法

Ⅲ．例题与练习

例1 已知一次函数y＝kx+b的图象经过点(3,5)和点(-4，-9),求当x＝5时，函数y的值．

分析 1．图象经过点(3,5)和点(-4，-9)，即已知当x＝3时，y＝5；x＝-4时，y＝-9．代入函数解析式中，求出k与b．

3、体会用“数形结合”思想解决数学问题．

教学重难点

待定系数法确定一次函数解析式

教学过程

Ⅰ．提出问题，创设情境

　 　一次函数关系式y＝kx+b(k≠0)，如果知道了k与b的值，函数解析式就确定了，那么有怎样的条件才能求出k和b呢？

问题1 已知一个一次函数当自变量x＝-2时，函数值y＝-1,当x＝3时，y＝-3．能否写出这个一次函数的解析式呢？

根据一次函数的定义，可以设这个一次函数为:y＝kx+b(k≠0),问题就归结为如何求出k与b的值．

由已知条件x＝-2时，y＝-1，得　 -1＝-2k+b．

由已知条件x＝3时，y＝-3， 得　 -3＝3k+b．

两个条件都要满足，即解关于x的二元一次方程

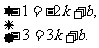　　 　　解得

所以，一次函数解析式为．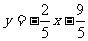

问题2 已知弹簧的长度y(厘米)在一定的限度内是所挂物质量x(千克)的一次函数．现已测得不挂重物时弹簧的长度是6厘米，挂4千克质量的重物时，弹簧的长度是7.2厘米,求这个一次函数的关系式．

考虑 这个问题中的不挂物体时弹簧的长度6厘米和挂4千克质量的重物时，弹簧的长度7.2厘米,与一次函数关系式中的两个x、y有什么关系？

Ⅱ．导入新课

上题可作如下分析：

已知y是x的函数关系式是一次函数，则关系式必是y＝kx+b的形式，所以要求的就是系数k和b 的值．而两个已知条件就是x和y的两组对应值，也就是当x＝0时，y＝6；当x＝4时，y＝7.2．可以分别将它们代入函数式，转化为求k与b 的二元一次方程组，进而求得k与b的值．

解 设所求函数的关系式是y＝kx+b(k≠0),由题意，得

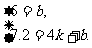
解这个方程组，得

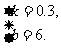
所以所求函数的关系式是y＝0.3x+6．(其中自变量有一定的范围)

讨论 1．本题中把两对函数值代入解析式后，求解k和b的过程，转化为关于k和b的二元一次方程组的问题．