1．提出问题，创设情境

　　 我们前面学习了有关一次函数的一些知识，掌握了其解析式的特点及图象特征，并学会了已知解析式画出其图象的方法以及分析图象特征与解析式之间的联系规律．如果反过来，告诉我们有关一次函数图象的某些特征，能否确定解析式呢？

这将是我们这节课要解决的主要问题，大家可有兴趣？

　　 Ⅱ．导入新课

　　 有这样一个问题，大家来分析思考，寻求解决的办法．

　　 [活动]

　　 活动设计内容：

　　 已知一次函数图象过点(3，5)与(-4，-9)，求这个一次函数的解析式．

　　 联系以前所学知识，你能总结归纳出一次函数解析式与一次函数图象之间的转化规律吗？

　　 活动设计意图：

　　 通过活动掌握待定系数法在函数中的应用，进而经历思考分析，归纳总结一次函数解析式与图象之间转化规律，增强数形结合思想在函数中重要性的理解．

　　 教师活动：

　　 引导学生分析思考解决由图象到解析式转化的方法过程，从而总结归纳两者转化的一般方法．

　　 学生活动：

　　 在教师指导下经过独立思考，研究讨论顺利完成转化过程．概括阐述一次函数解析式与图象转化的一般过程．

　　 活动过程及结论：

　　 分析：求一次函数解析式，关键是求出k、b值．因为图象经过两个点，所以这两点坐标必适合解析式．由此可列出关于k、b的二元一次方程组，解之可得．

　　 设这个一次函数解析式为y=kx+b．

　　 因为y=k+b的图象过点(3，5)与(-4，-9)，所以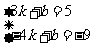

　　 解之，得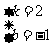

故这个一次函数解析式为y=2x-1。结论：

　　 像这样先设出函数解析式，再根据条件确定解析式中未知的系数，从而具体写出这个式子的方法，叫做待定系数法．

练习：

2．体验数形结合，逐步学习利用这一思想分析解决问题．

教学重点

待定系数法确定一次函数解析式．

教学难点

　　 灵活运用有关知识解决相关问题．

教学方法

　　 归纳─总结

教具准备

　　 多媒体演示．

　　 教学过程

1．经历待定系数法应用过程，提高研究数学问题的技能．

2．具体感知数形结合思想在一次函数中的应用

1．学会用待定系数法确定一次函数解析式．毛

　　 习题11．3─1、2、5、8题．

　　 本节课从解具体一元一次方程与当自变量x为何值时一次函数的值为0这两个问题入手，发现这两个问题实际上是同一个问题，进而得到解方程kx+b=0与求自变量x为何值时，一次函数y=kx+b值为0的关系，并通过活动确认了这个问题在函数图象上的反映．经历了活动与练习后让我们更熟练地掌握了这种方法．虽然用函数解决方程问题未必简单，但这种数形结合思想在以后学习中有很重要的作用

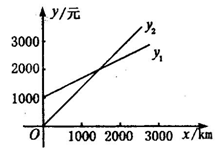
某单位急需用车，但又不准备买车，他们准备和一个体车主或一国有出租车公司其中一家签让合同．设汽车每月行驶x千米，应付给个体车主的月费用是y₁元，应付给出租车公司的月费用是y₂元，y₁、y₂分别是x之间函数关系如下图所示．每月行驶的路程等于多少时，租两家车的费用相同，是多少元？

用不同种方法解下列方程：

1．2x-3=x-2．　　 2．x+3=2x+1．

例1 一个物体现在的速度是5米／秒，其速度每秒增加2米／秒，再过几秒它的速度为17米／秒？

(两种解法)

补：例2　 利用图象求方程6x-3=x+2的解 ，并笔算检验

由图象可以看出直线y=6x-3与y=x+2交于点(1，3)，所以x=1