
2.画一次函数图象时,只要取几个点?怎样取比较简便?
1.一次函数的图象是什么形状呢?
2.在同个平面直角坐标系中画出下列函数的图象.
(1)y=-6x (2)y=-6x+5 (3)y=3x (4)y=3x+2
Ⅱ.导入新课
问题l:以上四个一次函数图象是什么形状呢?
让学生观察、讨论,得出四个函数的图象都是直线.
问题2:一次函数y=kx+b(k≠0)的图象都是一条直线吗?举例验证.
让学生猜想,举例验证,发现一次函数y=kx+b(k≠0)的图象是一条直线。指出这条直线通常也称为直线y=kx+b(b≠0),特别地,正比例函数y=kx(k≠0)的图象是经过(0,0)的一条直线.
问题3:几个点可以确定一条直线?
问题4:画一次函数图象时,只要取几个点?
只要取两点。今后画一次函数的图象,只要取两点再过两点画直线即可.
问题5:观察“做一做”画出的四个函数的图象,如图所示,比较下列各对一次函数的图象有什么共同点,有什么不同点.
(1)y=-6x与y=-6x+2
(2)y=x与y=x+2
(3)y=-6x+2与y=x+2
能否从中发现一些规律?
问题6:对于直线y=kx+b(k、b是常数,k≠0).常数k和b的取值对于直线的 位置各有什么影响?
让学生讨论,交流,然后填空:
两个一次函数,当k一样,b不一样时,有
共同点:__________________________
不同点:___________________________
当两个一次函数,b一样,k不一样时,有
共同点:__________________________
不同点:__________________________
在同一平面直角坐标系中画出下列函数的图象
(1)y=2x与y=2x+3 (2)y=2x+l与y=x+1
请同学们画出图象后,看看是否与上面的讨论结果一样.
Ⅲ.例题与练习
例1(1)作出一次函数y=-2x+5的图象,
(2)在所作的图象上取几个点,找出它们的横坐标和纵坐标,并验证它们是否满足关系式y=-2x+5。
列表:
|
x |
… |
-2 |
-1 |
0 |
1 |
2 |
… |
|
y=-2x+5 |
… |
9 |
7 |
5 |
3 |
1 |
… |
描点:以表中各组对应值作为点的坐标,在直角坐标第内描出相应的点。
连线:把这些点依次连接起来,得到y=-2x+5的图象,它是一条直线。
图象如下:
在图象上找点A(3,-1)B(4,-3),当x=3时,y=-2×3+5=-1;当x=4时,y=-2×4+5=-3。(3,-1),(4,-3)满足关系式y=-2x+5。
议一议
(1)满足关系式y=-2x+5的x、y所对应的点(x,y)都在一次函数y=-2x+5的图象上吗?
(2)一次函数y=-2x+5的图象上的点(x,y)都满足关系式y=-2x+5吗?
分组讨论,然后回答。
(1)满足关系式y=-2x+5的x,y所对应的点(x,y)都在一次函数y=-2x+5的图象上。
(2)一次函数y=-2x+5的图象上的点(x,y)都满足关系式y=-2x+5。
由此看来,满足函数关系式y=-2x+5的x,y所对应的点(x,y)都在一次函数y=-2x+5的图象上;反过来,一次函数y=-2x+5的图象上的点(x,y)都满足关系式y=-2x+5。所以,一次函数的代数表达式与图象是一一对应的,即满足一次函数的代数表达式的点在图象上,图象上的每一点的横坐标x,纵坐标y都满足一次函数的代数表达式。
例2 在同一平面直角坐标系中画出下列每组函数的图象.
(1)y=2x与y=2x+3;
(2)y=3x+1与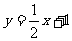 .
.
解

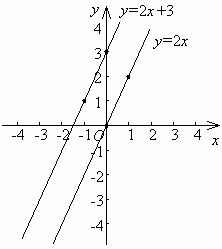

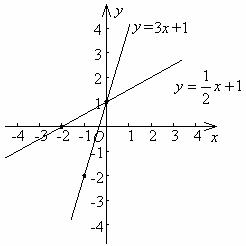
想一想 (1)上面每组中的两条直线有什么关系?(2)你取的是哪几个点,互相交流,看谁取的点比较简便.
结论:一般情况下,要取直线与x轴、y轴的交点比较简便.
例3 直线 分别是由直线
分别是由直线 经过怎样的移动得到的.
经过怎样的移动得到的.
分析 只要k相同,直线就平行,一次函数y=kx+b(k≠0)是由正比例函数的图象y=kx(k≠0)经过向上或向下平移 个单位得到的.b>0,直线向上移;b<0,直线向下移.
个单位得到的.b>0,直线向上移;b<0,直线向下移.
解  是由直线
是由直线 向上平移3个单位得到的;而
向上平移3个单位得到的;而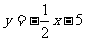 是由直线
是由直线 向下平移5个单位得到的.
向下平移5个单位得到的.
Ⅳ.课时小结
1、回顾作函数图象的一般步骤
前面我们已经学习了一次函数及正比例函数的概念,正比例函数与一次函数的关系,并能根据已知信息列出x与y的函数关系式,本节课我们研究一下一次函数的图象及性质。
1、 归纳作函数图象的一般步骤。
教学难点
理解一次函数的代数表达式与图象之间的对应关系。
教学过程
Ⅰ.提出问题,创设情境
1、能熟练地作出一次函数的图象。
2、能较熟练作出一次函数的图象。
教学重点
1、理解一次函数的代数表达式与图象之间的对应关系。
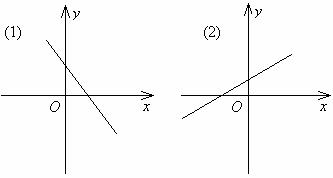
5.某个一次函数的图象位置大致如下图所示,试分别确定k、b的符号,并说出函数的性质.
4.已知点(-1,a)和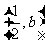 都在直线
都在直线 上,试比较a和b的大小.你能想出几种判断的方法?
上,试比较a和b的大小.你能想出几种判断的方法?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com