
1.形如y=kx(k是常数,k≠0)的函数叫做正比例函数,其中k叫比例系数.
正比例函数都是常数与自变量的乘积的形式.
11.2.1 正比例函数
知识库
3.当汽车距北京20千米时,汽车出发了多长时间?
解法一:用图象解答:
从图上可以看出4个小时可到达.
速度=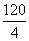 =30(千米/时).
=30(千米/时).
行驶1小时离开天津约为30千米.
当汽车距北京20千米时汽车出发了约3.3个小时.
解法二:用解析式来解答:
由图象可知:S与t是正比例关系,设S=kt,当t=4时S=120
即120=k×4 k=30
∴S=30t.
当t=1时 S=30×1=30(千米).
当S=100时 100=30t t=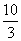 (小时).
(小时).
以上两种方法比较,用图象法解题直观,用解析式解题准确,各有优特点.毛
2.汽车行驶1小时,离开天津有多远?
1.汽车用几小时可到达北京?速度是多少?
2.y随x增大反而减小.
请你举出一个满足上述条件的函数,写出解析式,画出图象.
解:函数解析式:y=-0.5x
|
x |
0 |
2 |
|
y |
0 |
-1 |

板书设计
|
§11.2.1
正比例函数 一、正比例函数定义 二、正比例函数图象特征 三、正比例函数图象特征与解析式的关系规律 四、随堂练习 |
备课资料
汽车由天津驶往相距120千米的北京,S(千米)表示汽车离开天津的距离,t(小时)表示汽车行驶的时间.如图所示

1.它的图象是经过原点的一条直线.
2、 《课堂感悟与探究》
Ⅵ.活动与探究
某函数具有下面的性质:
1、 习题11.2─1、2、6题.
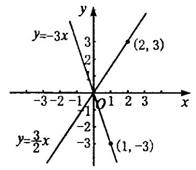
1.y=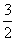 x 2.y=-3x
x 2.y=-3x
Ⅳ.课时小结
本节课我们通过实例了解了正比例函数解析式的形式及图象的特征,并掌握图象特征与关系式的联系规律,经过思考、尝试,知道了正比例函数不同表现形式的转化方法,及图象的简单画法,为以后学习一次函数奠定了基础.
Ⅴ.课后作业
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com