8．正比例函数y=kx(k为常数，k<0)的图象依次经过第________象限，函数值随自变量的增大而_________．

7．若x、y是变量，且函数y=(k+1)x^k2是正比例函数，则k=_________．

6．形如___________的函数是正比例函数．

5．已知(x₁，y₁)和(x₂，y₂)是直线y=-3x上的两点，且x₁>x₂，则y₁与y₂的大小关系是(　 )

　　 A．y₁>y₂　　　 B．y₁<y₂　　　 C．y₁=y₂ 　　D．以上都有可能

☆我能填

4．若函数y=(2m+6)x²+(1-m)x是正比例函数，则m的值是(　 )

　　 A．m=-3　　　 B．m=1　　 C．m=3　　　 D．m>-3

3．下列说法中不成立的是(　 )

　　 A．在y=3x-1中y+1与x成正比例； B．在y=-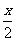中y与x成正比例

　　 C．在y=2(x+1)中y与x+1成正比例； D．在y=x+3中y与x成正比例

2．下列函数中，y是x的正比例函数的是(　 )

　　 A．y=4x+1　　　 B．y=2x²　　　 C．y=-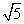x　　　 D．y=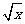

1．下列关系中的两个量成正比例的是(　 )

　 　A．从甲地到乙地，所用的时间和速度；　 B．正方形的面积与边长

　　 C．买同样的作业本所要的钱数和作业本的数量；D．人的体重与身高

3．根据两点确定一条直线，可以确定两个点(两点法)画正比例函数的图象．

　魔法师

　 　例1：已知y=(k+1)x+k-1是正比例函数，求k的值．

　　 分析：由正比例函数的定义可知k+1≠0且k-1=0即可

　 　解：根据题意得：k+1≠0且k-1=0，解得：k=1　 ∴k=1

　 　例2：根据下列条件求函数的解析式

　　 　①y与x²成正比例，且x=-2时y=12．

　　 　②函数y=(k²-4)x²+(k+1)x是正比例函数，且y随x的增大而减小．

　　 分析：①根据正比例函数的定义，可设y=kx²，然后由x=-2、y=12求得k的值．

　　 ②函数y=(k²-4)x²+(k+1)x是正比例函数；则k²-4=0，y随x的增大而减小，则k+1<0．

　　 解：①设y=kx²　 (k≠0)

　　 ∵x=-2时y=12　　 ∴(-2)²k=12　 ∴k=3　　 ∴y=3x²

　　 ②由题意得：k²-4=0　　 ∴k=2或k=-2

　　 ∵y随x的增大而减小，　 ∴k+1<0　 ∴k=-2　 ∴y与x的函数关系式是：y=-x

演兵场

　　 ☆我能选

2．正比例函数y=kx(k是常数，k≠0)的图象是一条经过原点的直线，我们通常称之为直线y=kx．

　　 当k>0时，直线y=kx依次经过第三、一象限，从左向右上升，y随x的增大而增大；

　　 当k<0时，直线y=kx依次经过第二、四象限，从左向右下降，y随x的增大而减小．