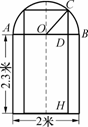
图14.2.3

分析由于厂门宽度足够，所以卡车能否通过，只要看当卡车位于厂门正中间时其高度是否小于CH．如图14.2.3所示，点D在离厂门中线0.8米处，且CD⊥AB， 与地面交于H．

解　 在Rt△OCD中，由勾股定理得

CD＝＝＝0.6米，

CH＝0.6+2.3＝2.9(米)＞2.5(米)．

因此高度上有0.4米的余量，所以卡车能通过厂门．

教师活动：分析例2，帮助学生寻找RT△OCD，强调应用方法

学生活动：听教师分析，积累实际应用经验

媒体使用：投影显示例2

教学形式：接受式

引导学生完成P58页“做一做”

课堂演练：

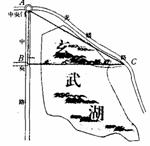
演练一：从地图上看(如图所示)，南京玄武湖东西向隧道与中央路北段及龙姗路大致成直角三角形．从B处到C处，如果直接走湖底隧道BC,将比绕道BAC(约.36km)和AC(约2. 95km)减少多少行程(精确到0.lkm)?

演练二：若△ABC的三边a、b、c满足条件

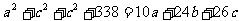
请你判断△ABC的形状.

教师活动：操作投影仪，显示“课堂演练”，启发、引导学生、关注“学困生”

学生活动：先独立完成，再有困难时，寻求同伴的帮助，通过交流，解决问题

2. 思路点拨：引导学生尝试着在自制的圆柱侧面上寻找最短路线，提醒学生将圆柱侧面展开成长方形，此时学生发现了“两点之间的所有连线中，线段最短”这个结论较易解决问题．

教师活动操作投影仪，启发、引导学生动手操作，通过感性认识来突破学生空间想像的难点．

学生活动：观察、拿出事先准备好的学具，边操作边讨论边理解，寻求解决问题的途径．

媒体使用：投影显示“问题情境”．

1、问题情境：如图14-2-1所示，有一个圆柱，它的高等于12厘米，底面半径等笼

3厘米，在圆柱下底面的A点有一点妈蚁，它想吃到上底面上与A点相对的B点处白

食物，沿圆柱侧面爬行的最短路程是多少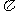？(的值取3)

(1)自制一个圆柱，尝试从A点到B点沿圆柱侧面画出几条路线，你认为哪条路寒

最短呢？图14-2-1(a)所示．

(2)如图14-2-1(b)，将圆柱侧面剪开展成一个长方形，从A点到B点的最短线路是什么？你画对了吗？

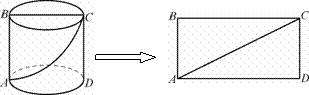
(3)蚂蚁从A点出发，想吃到B点上的食物，它沿圆柱侧面爬行的最短路程是多

少？

10．解：过点D作DE⊥AB于点E，

　　 则ED=BC=30m，EB=DC=1．4m．

　　 设AE=x米，在Rt△ADE中，∠ADE=30°，则AD=2x．

　　 由勾股定理，得AE²+ED²=AD²，

　　 即x²+30²=(2x)²，解得x≈17.32．

　　 ∴AB=AE+EB=17.32+1.4≈18.7(m)．

　　 答：树高AB约为18．7m．

　　 点拨：构造直角三角形，利用30°角所对的直角边等于斜边的一半和勾股定理建立方程．在利用勾股定理进行计算时，无直角三角形的情况下，可适当添加垂线构造直角三角形，并利用勾股定理．

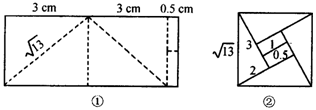
9．解：(1)设较长直角边为b，较短直角边为a，则小正方形的边长为：a-b．

而斜边即为大正方形边长，且其平方为13，即a²+b²=13①，

由a+b=5，两边平方，得a²+b²+2ab=25．

将①代入，得2ab=12．

所以(b-a)²=b²+a²-2ab=13-12=1．

即小正方形面积为1；

(2)由(2)题中矩形面积为6.5×2=13与(1)题正方形面积相等，仿照甲图可得，算出其中a=2，b=3，如图．

8．图略

7．48　 点拨：设底边长为2x，则腰长为16-x，有(16-x)²=8²+x²，x=6，

∴S=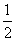×2x×8=48．

6．A　 点拨：设BD为x，则36-(2x)²=9-x²，x=3．

5．解：在直角三角形ADE中，由勾股定理，得DE²=AD²+AE²．

在直角三角形BEC中，由勾股定理，得EC²=BE²+BC²．

因为DE=EC，因此DE²=EC²，所以AD²+AE²=BE²+BC²．

所以15²+AE²=(25-AE)²+10²，解得AE=10(km)．

4．12米